Answers
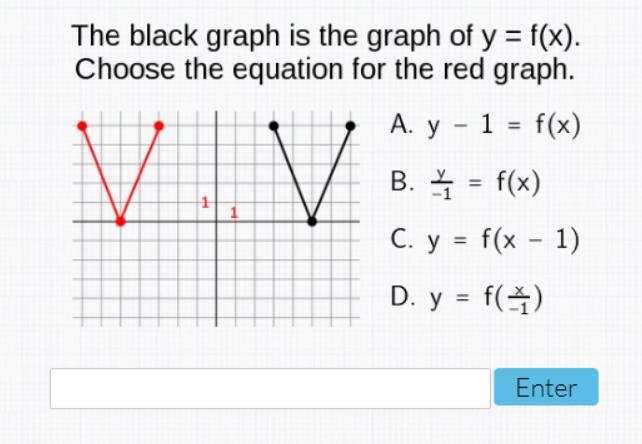
The red graph is the black graph reflected in the y axis, y = f(-x)
It's an odd way to write it, but the answer is:
Answer: D
Related Questions
Find the missing angle measures in the given rhombus.
Answers
Answer:
1 = 4 = 38°, 2 = 3 = 90°
Step-by-step explanation:
Because the diagonals of rhombi are perpendicular, ∠2 = ∠3 = 90°. Since the sum of angles in a triangle is 180°, ∠1 = 180° - 52° - 90° = 38°. If we look at the triangle with 1 and 4 as its base angles, we notice that it's an isosceles triangle, therefore ∠1 = ∠4 = 38°.
Answer:
Step-by-step explanation:
In rhombus, diagonals are perpendicular to each other.
∠2 = ∠3 = 90°
52° + ∠1 + ∠ 2 = 180° { Angle sum property of triangle}
52 + ∠1 + 90 = 180
∠1 + 142 = 180
∠1 = 180 - 142
∠1 = 38°
∠4 = ∠1 = 38° { Isosceles triangle}
I need help with this!
Answers
Part A
Answer: 33.2 degrees F
Explanation: Adding on a negative is the same as subtracting. So 72.3 + (-39.1) = 72.3 - 39.1 = 33.2
================================================
Part B
Answer: 70 + 2 + 0.3 + (-30) + (-9) + ( -0.1 )
Explanation:
Think of 72 as 70+2. Furthermore, think of 72.3 as 70+2+0.3; we just break the number up into its corresponding digits (adding zeros when needed). The 7 is in the tens place, the 2 is in the units or ones place, and the 3 is in the tenths place.
Similarly, we have 39.1 break down into 30+9+0.1, in which all three terms are made negative to represent -39.1
================================================
Part C
Answer: 70 + (-30) + 2 + (-9) + 0.3 + ( -0.1 )
Explanation: Arrange the tens place value items to be next to each other. Same goes for the units place value, and also the tenths place value.
================================================
Part D
Answer: [70 + (-30)] + [ 2 + (-9) ] + [ 0.3 + ( -0.1 ) ]
Explanation: Take the result of part C and surround each pair of terms in square brackets to show how the terms pair up.
How do I solve: 2 sin (2x) - 2 sin x + 2√3 cos x - √3 = 0
Answers
Answer:
[tex]\displaystyle x = \frac{\pi}{3} +k\, \pi[/tex] or [tex]\displaystyle x =- \frac{\pi}{3} +2\,k\, \pi[/tex], where [tex]k[/tex] is an integer.
There are three such angles between [tex]0[/tex] and [tex]2\pi[/tex]: [tex]\displaystyle \frac{\pi}{3}[/tex], [tex]\displaystyle \frac{2\, \pi}{3}[/tex], and [tex]\displaystyle \frac{4\,\pi}{3}[/tex].
Step-by-step explanation:
By the double angle identity of sines:
[tex]\sin(2\, x) = 2\, \sin x \cdot \cos x[/tex].
Rewrite the original equation with this identity:
[tex]2\, (2\, \sin x \cdot \cos x) - 2\, \sin x + 2\sqrt{3}\, \cos x - \sqrt{3} = 0[/tex].
Note, that [tex]2\, (2\, \sin x \cdot \cos x)[/tex] and [tex](-2\, \sin x)[/tex] share the common factor [tex](2\, \sin x)[/tex]. On the other hand, [tex]2\sqrt{3}\, \cos x[/tex] and [tex](-\sqrt{3})[/tex] share the common factor [tex]\sqrt[3}[/tex]. Combine these terms pairwise using the two common factors:
[tex](2\, \sin x) \cdot (2\, \cos x - 1) + \left(\sqrt{3}\right)\, (2\, \cos x - 1) = 0[/tex].
Note the new common factor [tex](2\, \cos x - 1)[/tex]. Therefore:
[tex]\left(2\, \sin x + \sqrt{3}\right) \cdot (2\, \cos x - 1) = 0[/tex].
This equation holds as long as either [tex]\left(2\, \sin x + \sqrt{3}\right)[/tex] or [tex](2\, \cos x - 1)[/tex] is zero. Let [tex]k[/tex] be an integer. Accordingly:
[tex]\displaystyle \sin x = -\frac{\sqrt{3}}{2}[/tex], which corresponds to [tex]\displaystyle x = -\frac{\pi}{3} + 2\, k\, \pi[/tex] and [tex]\displaystyle x = -\frac{2\, \pi}{3} + 2\, k\, \pi[/tex].[tex]\displaystyle \cos x = \frac{1}{2}[/tex], which corresponds to [tex]\displaystyle x = \frac{\pi}{3} + 2\, k \, \pi[/tex] and [tex]\displaystyle x = -\frac{\pi}{3} + 2\, k \, \pi[/tex].Any [tex]x[/tex] that fits into at least one of these patterns will satisfy the equation. These pattern can be further combined:
[tex]\displaystyle x = \frac{\pi}{3} + k \, \pi[/tex] (from [tex]\displaystyle x = -\frac{2\,\pi}{3} + 2\, k\, \pi[/tex] and [tex]\displaystyle x = \frac{\pi}{3} + 2\, k \, \pi[/tex], combined,) as well as[tex]\displaystyle x =- \frac{\pi}{3} +2\,k\, \pi[/tex].Island A is 250 miles from island B. A ship captain travels 260 miles from island A and then finds out he is off course and 160 miles from island B. What bearing should he turn to, so he is heading to island B?
Answers
CHECK THE COMPLETE QUESTION BELOW
Island A is 250 miles from island B. A ship captain travels 260 miles from island A and then finds that he is off course and 160 miles from island B. What bearing should he turn to, so he is heading straight towards island B?
A. 111.65
B. 119.84
C. 21.65
D. 135.53
Answer:
OPTION A IS CORRECT
A. 111.65
Step-by-step explanation:
This question can be explained using a triangle, let us say triangle ABD
and let us say A and B represent the islands and D is the particular point from where the captain is standing at a distance of 160 miles from B island .
We will be making use of cosines rule to calculate our angles, and we know that from cosine rule
D² = a² + b² -2abCosD
Where, a= 160 b = 260 and d = 250 then we can substitute in order to calculate our angles
250²= 60² + 260² - 2(160*260)Cos(D)
62500= 625600+ 67600- 83200CosD
83200CosD= 25600+ 67600 - 625600
83200CosD= 30700
CosD= 30700/83200
CosD= 0.369
D= cos⁻¹ (0.369)
D=68.35
Therefore, the angle inside the triangle is 68.35°
Now we can now find the bearing the captain supposed to turn , if he is heading to island B which will be the external angle of the triangle, but we know that The external angle =180°(supplimentary angles )
Then the angle he would turn will be external angle of the triangle - 68.35°
= (180 - 68.35)
= 111.65°
Therefore, the bearing the captain should turn is 111.65° for him to be heading straight towards island B.
Solve each problem below. Show all working in the space provided.
1. A square shed measures 8m 35cm along each side. Find the perimeter of th
shed.
Answer:
Answers
Answer:
33m 40cm.
Step-by-step explanation:
One side of the shed measures 8 meters and 35 centimetres, which is 800 + 35 = 835 centimetres.
Since the shed is a square, all side lengths are 835 centimetres long. So, the perimeter is 835 * 4 = 3,340 centimetres. That means that the perimeter is 33 meters and 40 centimetres.
Hope this helps!
Coffee is sold in two different sized canisters. The smaller canister has a diameter of 9 cm and a height of 12 cm. The larger canister is double the size of the small canister (i.e., the diameter and height are doubled). Calculate the volume and surface area of each canister and compare the results of doubling the dimensions.
Answers
Answer:
This means volume of the larger canister is 8 times more than volume of the smaller canister.
This means surface area of the larger canister is 4 times greater than volume of the smaller canister.
Step-by-step explanation:
Smaller canister
Diameter=9cm
Radius=diameter/2
=9/2=4.5cm
Height=12cm
Larger canister (double of the smaller canister)
Radius=4.5*2=9cm
Height=12*2=24cm
Volume=πr^2h
Surface area=2πrh + 2πr^2
Volume of smaller canister=πr^2h
=3.14*(4.5)^2*12
=3.14*20.25*12
=763.02
Surface area of the smaller canister=2πrh + 2πr^2
=2*3.14*4.5*12 + 2*3*14*(4.5)^2
=339.12 + 127.17
=466.29
Volume of larger canister=πr^2h
=3.14*(9)^2*24
=3.14*81*24
=6104.16
Surface area of larger canister=2πrh + 2πr^2
=2*3*14*9*24 + 2*3.14*(9)^2
=1356.48 + 508.68
=1865.16
Compare smaller and larger volume of the canister:
Volume if larger/volume of smaller
=6104.16/763.02
=8
This means volume of the larger canister is 8 times more than volume of the smaller canister
Compare surface area of larger and smaller canister:
Surface area of larger canister/surface area of smaller canister=1865.16/466.29
=4
This means surface area of the larger canister is 4 times greater than volume of the smaller canister
Answer:
Yeah, what she said above.
Step-by-step explanation:
How many solutions does the nonlinear system of equations below have?
Answers
Answer:
OneStep-by-step explanation:
There is only one intercepting point, it means one solution.
A city survey of two neighborhoods asked residents whether they would prefer a new playground or a dog park.
Answers
Answer:
so if it is asking about the exact percentage then the answer is B but if it is the percentage in all the answer is D.
Step-by-step explanation: My reasoning behind is that 70 percent of the neighborhood wants a playground if it is 40 to 17
Percentage Hill point residence want playground is about 70% .
What is percentage?A percentage is a number or ratio expressed as a fraction of 100. It is often denoted using the percent sign, "%"
According to the question
Hill point residence want playground = 0.40
Total who want playground = 0.58
now,
Percentage Hill point residence want playground over total
[tex]\frac{0.40}{0.58} *100[/tex]
= 68.96%
≈ 70%
Hence, Percentage Hill point residence want playground is about 70% .
To know more about Percentage here:
https://brainly.com/question/16797504
#SPJ2
What is the approximate perimeter of the figure?
Answers
Answer:
7.1 inches
Step-by-step explanation:
perimeter you go round from apointof your choice so
add 2+2=4
then apply 1/4πd for the round part
d=4 and it's quarter a circle then add them together
Answer:
7.1 inches
Step-by-step explanation:
To find the perimeter of the circle you would need to follow the formula: 2piR. Since r=2, 2*2=4. So 4 multiplied by pi (3.14 or 22/7). Since this is a quarter of a circle you would divide the answer 12.56 by four which equals 3.14. Now just add the extra two 2s left on the flat sides of the figure which ends up with your answer of 7.14 OR 7.1.
Hope this helps!! <3
[4 + (3 – 1)]3 = ? A. 12 B. 32 C. 64 D. 128 E. 216
Answers
Answer:
18
Step-by-step explanation:
Answer:
18.
Step-by-step explanation:
[4 + (3 - 1)] * 3
= (4 + 2) * 3
= 6 * 3
= 18
Hope this helps!
Isosceles trapezoid ABCD is inscribed in ⊙O with radius 5. AD=6 and the median of ABCD has length 7. Find the distance from AD to BC. this was the only info given!
Answers
Answer:
The distance from AD to BC is 7
Step-by-step explanation:
The information given are;
The type of inscribed quadrilateral ABCD = Isosceles trapezoid
The radius of the circle = 5
Segment AD of ABCD = 6
The median of the trapezoid ABCD = 7
Given the trapezoid theorem, the median is equal to half the length of the two bases added together, we have;
(AD + BC)/2 = 7
Which gives;
(6 + BC)/2 = 7
BC = 7×2 - 6 = 8
Therefore the distance from AD to BC is given by the distance from BC to the median line added to the distance from AD to the median line given as follows;
The distance from BC to the median = √(Radius² - (BC/2)²) = √(5² - (8/2)²) = 3
The distance from BC to the median = 3
The distance from AD to the median = √(Radius² - (AD/2)²) = √(5² - (6/2)²) = 4
Which gives;
The distance from AD to BC = 3 + 4 = 7
Find each product.
(X3+2x2)x4
PLEASE HELP!!! ASAP!!!
Answers
Answer:
4x^3+8x^2
Step-by-step explanation:
Multiply each term:
4x^3+8x^2
PLZ MARK ME BRAINLIEST
Please answer this question now
Answers
Answer:
36°
Step-by-step explanation:
<U + < V + <W = 180° (sum of angles in a triangle)
<W = 54°
The tangent is always perpendicular to the radius drawn to the point of tangency...
therefore,
<U = 90°
90° + <V + 54° = 180°
144° + <V = 180°
<V = 180° - 144°
<V = 36°
Answer:
V=36
Step-by-step explanation:
tangent makes rigt angle with radius angle U=90
W+V+U=180
V=180-90-54
V=36
Point A is at (-6,6) and point C is at (-6,-2). Find the coordinates of point B on Ac such that AB =3/4AC
Answers
Answer:
B(-6, 0)
Step-by-step explanation:
You want to find B such that ...
(B -A) = (3/4)(C -A) . . . . the required distance relation
4(B -A) = 3(C -A) . . . . . . multiply by 4
4B = 3C +A . . . . . . . . . . add 4A, simplify
Now, we can solve for B and substitute the given coordinates:
B = (3C +A)/4 = (3(-6, -2) +(-6, 6))/4 = (-24, 0)/4 = (-6, 0)
The coordinates of point B are (-6, 0).
Answer:
the answer your looking for is (-3,-3)
Step-by-step explanation:
Coffee is sold in two different sized canisters. The smaller canister has a diameter of 9 cm and a height of 12 cm. The larger canister is double the size of the small canister (i.e., the diameter and height are doubled). Calculate the volume and surface area of each canister and compare the results of doubling the dimensions.
Answers
Answer:
The larger canister has 8 times the volume and 4 times the volume of the smaller one.
Step-by-step explanation:
The smaller canister has a diameter of 9 cm (radius = 4.5 cm) and height of 12 cm.
The larger canister has double the diameter and height of the smaller one. The diameter of the larger canister is 18 cm (radius = 9 cm) and height of 24 cm.
The canisters are in the shape of a cylinder.
The volume of a cylinder is given as:
[tex]V = \pi r^2h[/tex]
The surface area of a cylinder is given as:
A = 2πr(r + h)
SMALLER CANISTER
Volume = π * 4.5 * 4.5 * 12 = 763.41 cubic centimetres
Area = 2 * π * 4.5(4.5 + 12) = 2 * π * 4.5 * 16.5 = 466.53 square centimetres
LARGER CANISTER
Volume = π * 9 * 9 * 24 = 6107.26 cubic centimetres
Area = 2 * π * 9(9 + 24) = 2 * π * 9 * 33 = 1866.11 square centimetres
By reason of comparison, the larger canister has 8 times the volume and 4 times the volume of the smaller one despite having double the dimensions.
Answer:
Yeah, what they said above.
Step-by-step explanation:
The summer has ended and it’s time to drain the swimming pool. 20 minutes after pulling the plug, there is still 45 000L of water in the pool. The pool is empty after 70 minutes. Calculate the rate that the water is draining out of the pool. (Hint: remember this line is sloping down to the right) b) Calculate how much water was in the pool initially (at time 0). I think it was 80 000 c) Write an equation for this relationship. d) Use your equation to calculate how much water is in the pool at 62 minutes.
Answers
Step-by-step explanation:
At t = 20 min, V = 45,000 L.
At t = 70 min, V = 0 L.
a) The rate is the slope:
m = ΔV/Δt
m = (0 L − 45,000 L) / (70 min − 20 min)
m = -900 L/min
b) Using the slope to find V when t = 0 min:
m = ΔV/Δt
-900 L/min = (V − 0 L) / (0 min − 70 min)
V = 63,000 L
c) Use slope-intercept form to find the equation.
V = -900t + 63,000
d) At t = 62 min:
V = -900(62) + 63,000
V = 7200
Answer:
a. -900 L/min
b. Vo = 63,000 Liters
c. V ( t ) = 63,000 - 900*t
d. 7,200 Liters
Step-by-step explanation:
Solution:-
We have a swimming pool which is drained at a constant linear rate. Certain readings were taken for the volume of water remaining in the pool ( V ) at different instances time ( t ) as follows.
t = 20 mins , V = 45,000 Liters
t = 70 mins , V = 0 Liters
To determine the rate ( m ) at which water drains from the pool. We can use the linear rate formulation as follows:
[tex]m = \frac{V_2 - V_1}{t_2 - t_1} \\\\m = \frac{0 - 45000}{70 - 20} \\\\m = \frac{-45,000}{50} = - 900 \frac{L}{min}[/tex]
We can form a linear relationship between the volume ( V ) remaining in the swimming pool at time ( t ), using slope-intercept form of linear equation as follows:
[tex]V = m*t + V_o[/tex]
Where,
m: the rate at which water drains
Vo: the initial volume in the pool at time t = 0.
We can use either of the data point given to determine the initial amount of volume ( Vo ) in the pool.
[tex]0 = -900*( 70 ) + V_o\\\\V_o = 63,000 L[/tex]
We can now completely express the relationship between the amount of volume ( V ) remaining in the pool at time ( t ) as follows:
[tex]V ( t ) = 63,000 - 900*t[/tex]
We can use the above relation to determine the amount of volume left after t = 62 minutes as follows:
[tex]V ( 62 ) = 63,000 - 900*(62 )\\\\V ( 62 ) = 63,000 - 55,800\\\\V ( 62 ) = 7,200 L[/tex]
An air traffic controller spots two airplanes at the same altitude converging to a point as they fly at right angles to each other. One airplane is 150 miles from the point and has a speed of 300 miles per hour. The other is 200 miles from the point and has a speed of 400 miles per hour.
(a) At what rate is the distances between the planes decreasing?
(b) How much time does the air traffic controller have to get one of the planes on a different flight path?
Answers
Answer:
(a) D(t) = 250t -500 miles
(b) Controller has 2 hours, but including time for pilots to divert course or altitude.
Step-by-step explanation:
Given:
two planes at same altitude heading in a collision course.
Plane A at 400 miles from collision point at 200 mph
Plane B at 300 miles from collision point at 150 mph.
Theoretical collision happens in
t = 400/200 = 300/150 = 2 hours
Distance ya of plane A from collision point as a function of time in hours
ya(t) = 400 -200t
Distance yb of plane B from collision point as a function of time in hours
yb(t) = 300-150t
(a) Distance between two planes,
Since the two planes are on courses perpendicular to each other, will need using pythagorean theorem
D(t) = sqrt(ya(t)^2+yb(t)^2)
= sqrt((400-200t)^2+(300-150t)^2)
= 250(t-2)
D(t) = 250t -500 miles
b. time available
Time until D(t) = 0
solve D(t) = 0
D(t) = 0
250(t-2) = 0
t = 2 (two hours)
Answer:
a) -500 mph
b) 1/2 h
Step-by-step explanation:
a)[tex]\frac{ (150(-300))+(200(-400))}{\sqrt{150x^{2} +200^{2} } }[/tex]
b) [tex]\frac{\sqrt{150^{2}+200^{2} } }{500}[/tex]
I need the answer in degrees
Answers
Answer:
x = 69°Step-by-step explanation:
Angles at a point add up to 360°
To find x add up all the angles and equate them to 360°
That's
168 + 123 + x = 360
291 + x = 360
x = 360 - 291
x = 69°
Hope this helps you
Answer:
x = 69
Step-by-step explanation:
The sum of a circle is 360 degrees
x+ 168+123 = 360
Combine like terms
x +291 = 360
Subtract 291 from each side
x+291-291 = 360-291
x =69
There are 20 players on a soccer team. From them, a captain and an alternate captain have to be chosen. How many possibilities are there?
Answers
Answer: The number of possibilities = 380
Step-by-step explanation:
Given, There are 20 players on a soccer team. From them, a captain and an alternate captain have to be chosen.
Since, captain and alternate captain comes in order.
Number of ways to choose r things out of n things (when order matters) :
[tex]^nP_r=\dfrac{n!}{(n-r)!}[/tex]
Number of ways to choose 2 players ( for captain and alternate captain ) from 20 players :
[tex]^{20}P_2=\dfrac{20!}{18!}=20\times19=380[/tex]
Hence, the number of possibilities = 380
You have 0.895 m of ribbon to hang the “Grand Opening” sign. You need 100 cm to hang it correctly. Do you have enough ribbon? If not,how much more do you need?
Answers
Answer:
no you need 10.5cm
Step-by-step explanation:
so convert 0.895m to cm by multiplying it by 100 to get 89.5 which is less
so take the required 100-89.5
Subtraction is a mathematical operation. The ribbon is not enough. 10.5 cm of ribbon is more needed.
What is subtraction?Subtraction is a mathematical operation that reflects the removal of things from a collection. The negative symbol represents subtraction.
It is known that 1 meter is equal to 100cm, therefore, the length of the ribbon will be equal to,
[tex]\rm 1\ m =100\ cm\\\\0.895\ m = 0.895 \times 100 = 89.5\ cm[/tex]
Now, as the ribbon needed is 100 cm, therefore, the length of ribbon that is needed more is
[tex]\rm \text{length of the ribbon needed} = 100\ cm - 89.5\ cm = 10.5\ cm[/tex]
No, the ribbon is not enough. 10.5 cm of ribbon is more needed.
Learn more about Subtraction:
https://brainly.com/question/1927340
#SPJ2
A triangle has sides 45, 4x and 2x−4. What is the possible range of x?
Answers
Answer: I think it's 2
Step-by-step explanation: i am not dat good at math
The cost of importing five dozen china dinner sets, billed at $32 per set, and paying a duty of 40%, is
Answers
Answer:
duty = 64
Total cost is 224
Step-by-step explanation:
First find the cost of the 5 sets
5 * 32 = 160
Then find the duty
160 * 40%
160 * .4 = 64
Add this to the cost of the sets
160+64 =224
Which system of equations has the solution shown in the graph? A. y = -5x + 1 and y = -x + 5 B. y = 5x + 1 and y = -x − 5 C. y = 5x − 1 and y = -x + 5 D. y = -5x − 1 and y = -x − 5
Answers
Answer:
C. y = 5x-1 and y = -x+5Step-by-step explanation:
Since there are two lines on the graph, we will find the equation of both lines. The standard form of equation of a line is y = mx+c where;
m is the slope of the line = y₂-y₁/x₂-x₁
c is the intercept (the point where the line cuts the y axis)
For the blue line;
It can be seen that the coordinate of the lines are (1,4) and (0, -1)
m = -1-4/0-1
m = -5/-1
m = 5
For this line, it can be seen that the line cuts the y-axis at -1, hence the intercept of the line is -1
The equation of the blue line will be y = 5x+(-1)
y = 5x-1
For the red line;
It can be seen that the coordinate of the lines are (0,5) and (5, 0)
m = 0-5/5-0
m = -5/5
m = -1
For this line, it can be seen that the line cuts the y-axis at 5, hence the intercept of the line is 5
The equation of the red line will be y = -x+5
Hence, the system of equations that has the solution shown in the graph are y = 5x-1 and y = -x+5
WILL MARK BRAINLIEST
Answers
Answer:
A
Step-by-step explanation:
A rectangular tank with a square base, an open top, and a volume of 10,976 ft cubed is to be constructed of sheet steel. Find the dimensions of the tank that has the minimum surface area.
Answers
Answer:
Dimensions to minimize surface are is 28 ft x 28 ft x 14 ft
Step-by-step explanation:
The Volume of a box with a square base of say;x cm by x cm and height
h cm is;
V = x²h
Now, the amount of material used is directly proportional to the surface area, hence we will minimize the amount of material by minimizing the surface area.
The formula for the surface area of the box described is given by;
A = x² + 4xh
However, we need A as a function of
only x, so we'll use the formula;
V = x²h
V = x²h = 10,976 ft³
So,
h = 10976/x²
So,
A = x² + 4x(10976/x²)
A = x² + 43904/x
So, to minimize the area, it will be at dA/dx = 0.
So,
dA/dx = 2x - 43904/x² = 0
Factorizing out, we have;
2x³ = 43904
x³ = 43904/2
x³ = 21952
x = ∛21952
x = 28 ft
since, h = 10976/x²
h = 10976/28² = 14 ft
Thus,dimension to minimize surface are is 28 ft x 28 ft x 14 ft
PLEASE HELP! 20 POINTS!!
(c) Analysts predict the share price of a new company, Hydrate Energy, to be modelled by the equation
V = 2.95 + 2log10 (10t + 1) where t is the number of years and V is the value in dollars.
(i) How much do they expect the share price to increase in value between the first and third years?
Show working
Answers
Answer:
The share price increased by $40
Step-by-step explanation:
In the first year: (t = 1)
=> V = [tex]2.95 +2log10(10(1)+1)[/tex]
=> [tex]V = 2.95 + 2 (10+1)\\V = 2.95+2(11)[/tex]
=> [tex]V = 2.95+22[/tex]
=> V = $ 24.95
In the 3rd Year: (t = 3)
=> [tex]V = 2.95 + 2log10(10(3)+1)[/tex]
=> [tex]V = 2.95+ 2(30+1)[/tex]
=> [tex]V = 2.95+2(31)[/tex]
=> V = 2.95 + 62
=> V = $64.95
The Share Price increased by:
=> $64.95-$24.95
=> $40
The share price increased by $40
Answer this question
Answers
Answer:
1.
a) exact form: -1 /14 or decimal form: -0.0714285
b) exact form: -23/120 or decimal form: -0.1916
2.
a) 89
b)98
c) 5.7
d) 4.8
3.
i) 2*2*2*2*2*2*3*3*3
ii) 3*3*3*5*5*5
iii) 2*2*2*2*2*2*2*2*2*2*2*2
iv) 2*2*2*2*2*2*5*5*5
9.
i) x = -9
ii) x + 1/7
I hope this helps get you started :)
how many unique planes can be determined by four noncoplanar points?
Answers
Answer:
Four unique planes
Step-by-step explanation:
Given that the points are non co-planar, triangular planes can be formed by the joining of three points
The points will therefore appear to be at the corners of a triangular pyramid or tetrahedron such that together the four points will form a three dimensional figure bounded by triangular planes
The number of triangular planes that can therefore be formed is given by the combination of four objects taking three at a time as follows;
₄C₃ = 4!/(3!×(4-3)! = 4
Which gives four possible unique planes.
Which letter of the alphabet is next in the series?
J O T Y D
(A) I (B) J (C) K (D) L
Answers
Answer:
A
i
Step-by-step explanation:
Hope it helps
BRAINLEST Use the function f(x) = 2x^2 − 5x + 3 to answer the questions. Part A: Completely factor f(x). Part B: What are the x-intercepts of the graph of f(x)? Show your work.
Answers
Answer:
answer pic below :)
Step-by-step explanation: