Answers
Answer:
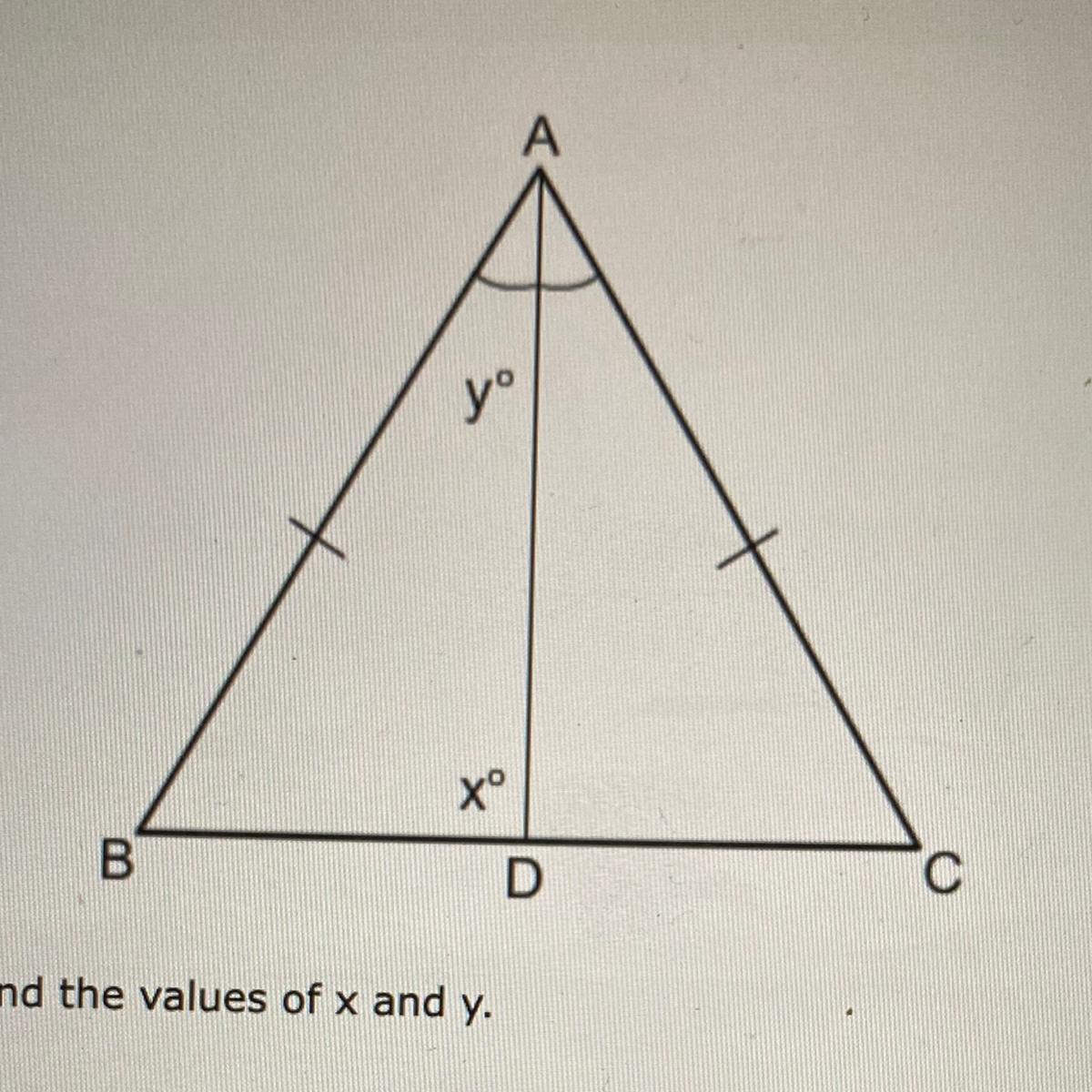
x=90 degrees and y=41 degrees.
Step-by-step explanation:
In the diagram
[tex]AB=AC\\$Therefore \triangle ABC$ is an isosceles triangle[/tex]
[tex]m\angle C=49^\circ[/tex]
Since ABC is Isosceles
[tex]m\angle B=m\angle C=49^\circ $ (Base angles of an Isosceles Triangle)[/tex]
[tex]m\angle A+m\angle B+m\angle C=180^\circ $ (Sum of angles in a Triangle)\\m\angle A+49^\circ+49^\circ=180^\circ\\m\angle A=180^\circ-(49^\circ+49^\circ)\\m\angle A=82^\circ[/tex]
[tex]m\angle x=90^\circ $(perpendicular bisector of the base of an isosceles triangle)[/tex]
[tex]m\angle y=m\angle A \div 2 $ (perpendicular bisector of the angle at A)\\m\angle y=82 \div 2\\m\angle y=41^\circ[/tex]
Therefore:
x=90 degrees and y=41 degrees.
Related Questions
Five times a number is divided by $7$ more than the number. If the result is $2$, then what was the original number? please help!
Answers
Answer:
3
Step-by-step explanation:
Because the number 5 is a number that you get from 7 more than n, and 2 is the other divisor that means n must equal 10 and 7 less than 10 is 3.
When five times a number is divided by 7 more than the number and the result is 2, then the number is 14/3, which is solved using the linear equation in one variable 5x/(x+ 7) = 2, where x is the required number.
What are linear equations in one variable?Linear equations are first-order equations. Lines in the coordinate system are determined by linear equations. A linear equation in one variable is defined as an equation with a homogeneous variable of degree 1 (i.e. only one variable).
How to solve the given question?In the question, we are asked to find a number, which satisfies the statement, "Five times a number is divided by 7 more than the number. The result of this division is 2".
We assume the number to be x.
Now we try to form a linear equation in one variable from the given statement.
Five times a number is 5x.
7 more than a number is x + 7.
We are said that five times a number is divided by 7 more than a number. This can be shown as 5x/(x + 7).
Now, the result is given as 2, which can be shown as:
5x/(x+ 7) = 2, which is the required linear equation in one variable.
To get the number, we solve the equation using the following steps:
5x/(x+ 7) = 2
or, {5x/(x+ 7)}*(x + 7) = 2*(x + 7) (Multiplying both sides by (x + 7))
or, 5x = 2x + 14 (Simplifying)
or, 5x - 2x = 2x + 14 - 2x (Subtracting 2x from both sides)
or, 3x = 14 (Simplifying)
or, 3x/3 = 14/3 (Dividing both sides by 3)
or, x = 14/3 (Simplifying)
∴ When five times a number is divided by 7 more than the number and the result is 2, then the number is 14/3, which is solved using the linear equation in one variable 5x/(x+ 7) = 2, where x is the required number.
Learn more about the linear equation in one variable at
https://brainly.com/question/24145091
#SPJ2
Which value for x makes the sentence true?
3/4x+ 4 = 7
1)4
2) 44/3
3) -3
4) 8
Answers
Answer:
x=4
Step-by-step explanation:
3/4x+ 4 = 7
Subtract 4 from each side
3/4x+ 4-4 = 7-4
3/4x = 3
Multiply each side by 4/3
4/3 * 3/4 x = 3 * 4/3
x = 4
The principal P is borrowed at a simple interest rate r for a period of time t. Find the simple interest owed for the use of the money. Assume there are 360 days in a year. P = $7000, r = 0.2%, t = 6months
Answers
Answer:
$7
Step-by-step explanation:
Simple interest formula:
I = Prt
6 months = 6 * 30 days = 180 days
1 year = 360 days
t = (180 days)/(360 days) = 0.5
I = $7000 * 0.002 * 0.5
I = $7
Answer:
$7
Step-by-step explanation:
Recall that simple interest is given by
I = Prt,
Where :
I = interest (we are asked to find this)
P = principal amount = given as $7000
r = rate = given as 0.2% = 0.002
t = time in years = given as 6 months = 0.5 years
SImply substitute the known values into the equation above:
I = Prt
= (7000)(0.002)(0.5)
= $7
Calculate the volume of a cube with sides measuring 2.5 metres
Answers
Answer:
15.625 m³
Step-by-step explanation:
The volume of a cube has a formula: V = a³
V = volume
a = side length
The side length is given 2.5 meters.
V = 2.5³
Solve for V.
V = 15.625
The volume is 15.625 cubic meters.
Answer:
15.625cm^3
Step-by-step explanation:
Formula:
V=lxwxh
Given:
l=2.5m
w=2.5m
h=2.5m
Answer:
V=lxwxh
V=2.5m*2.5m*2.5m
V=6.25m^2*2.5m
V=15.625m^3
Hope this helps :)
What is the quotient? URGENT!!
Answers
Answer:
The answer is A.
Step-by-step explanation:
You have to multiply by converting the second fraction into upside down :
[tex] \frac{4x + 1}{6x} \div \frac{x}{3x - 1} [/tex]
[tex] = \frac{4x + 1}{6x} \times \frac{3x - 1}{x} [/tex]
[tex] = \frac{(4x + 1)(3x - 1)}{x(6x)} [/tex]
[tex] = \frac{12 {x}^{2} - 4x + 3x - 1}{6 {x}^{2} } [/tex]
[tex] = \frac{12 {x}^{2} - x - 1 }{6 {x}^{2} } [/tex]
Good Morning can I get some help please?
Answers
Answer:
it is A!! hope this helped mark brainly
Two ballpoint pens are selected at random from a box that contains3 blue pens, 2 red pensand 3 green pens. If X is the number of blue pens
Answers
Answer: 3/(28) ≈ 10.7%
Step-by-step explanation:
3 blue + 2 red + 3 green = 8 total pens
First pick and Second pick
[tex]\dfrac{3\ blue\ pens}{8\ total\ pens}\quad \times \quad \dfrac{2\ remaining\ blue\ pens}{7\ remaining\ total\ pens}\quad =\large\boxed{\dfrac{3}{28}}[/tex]
slope=4/3 find the equation of the parallel line through (5,5)
Answers
Answer:
[tex]y=\frac{4}{3}x-1.75[/tex]
Step-by-step explanation:
If the slope of a line is 4/3,
and we wanna find the equation of a line that is parallel to it and crosses through (5,5).
So we already have the slope because the slope of 2 parallel lines are the same.
y = 4/3x
Look at the image below↓
So now we just need to find the y-intercept.
After some numbers we got,
[tex]y=\frac{4}{3}x-1.75[/tex]
Look at the other image below↓
Thus,
the equation of the parallel line is [tex]y=\frac{4}{3}x-1.75[/tex].
Hope this helps :)
6th grade math, help me please:)
Answers
Answer:
21
Step-by-step explanation:
Just like a dilation you want to find some sort of scale factor. Now when 7/2 is simplified it then becomes 3.5. Now multiply that by 6 since we are trying to find the ratio. when multiplied by 6 it becomes 21 so the ration of wins to losses is 21/6
You weigh six packages and find the weights to be 26, 18,58,22,54,and 50 ounces. If you include a package that weighs 66 ounces, which will increase more, the median or the mean?
Answers
Answer:
Step-by-step explanation:
The mean which is also known as the average is determined by dividing the sum of the weight of the packages by the total number of packages. From the information given,
Mean = (26 + 18 + 58 + 22 + 54 + 50)/6 = 38
If you include a package that weighs 66 ounces, the new mean would be
New mean = (26 + 18 + 58 + 22 + 54 + 50 + 66)/7 = 42
For the median, we would rearrange the weights in ascending order. It becomes
18, 22, 26, 50, 54, 58
Median = (26 + 50)/2 = 38
By adding the new weight, it becomes
18, 22, 26, 50, 54, 58, 66
New median = 50
It can be seen that both the median increased by more. It increased by 12 while the mean increased by 4
Answer: The mean which is also known as the average is determined by dividing the sum of the weight of the packages by the total number of packages. From the information given, Mean = (26 + 18 + 58 + 22 + 54 + 50)/6 = 38If you include a package that weighs 66 ounces, the new mean would be New mean = (26 + 18 + 58 + 22 + 54 + 50 + 66)/7 = 42For the median, we would rearrange the weights in ascending order. It becomes18, 22, 26, 50, 54, 58Median = (26 + 50)/2 = 38By adding the new weight, it becomes18, 22, 26, 50, 54, 58, 66New median = 50It can be seen that both the median increased by more. It increased by 12 while the mean increased by 4
Step-by-step explanation:
Given the equation (x−13)2+y2=64, identify the center and radius. Do not enter any spaces when typing your answers.
Answers
Answer:
centre = (13,0)
radius = 8
Step-by-step explanation:
The standard equation of the circle is
(x-x0)^2 + (y-y0)^2 = r^2 ...............(1)
where
(x0,y0) is the centre,
r is the radius.
For
(x-13)^2 + y^2 = 64 ..............(2)
we rewrite (2)
(x-13)^2 + (y-0)^2 = 8^2 ...............(3)
and compare (3) with (1)
to identify
x0 = 13, y0 = 0, and r = 8
Therefore
centre = (13,0)
radius = 8
hey guys can you please help me with this. i’m really desperate please help anything helps. thank u :(
Answers
Answer:
- 29 / 20
Step-by-step explanation
The cosec (x) = 1 / sin(x)
There are 2 ways to do this:
Either using a calculator:
sin^-1(20 / 29) = 43.60281897
so inputting into 1/sin(-x) where x = 43.6.....
This gives: -29 / 20
OR
1 / sin(x) = cosec ( x)
so cosec (x) = 1/(20/29)
= 29/20
By observing the cosec(x) graph, we see that to get cosec (-x), all we need to do is to minus our answer seeing as the graph is symmetrical across the axes. Therefore x = -29/20
k/4 + 3= 14 k = pls help
Answers
Answer:
k = 44
Step-by-step explanation:
k/4 + 3 = 14
k/4 = 11
k = 44
Answer:
[tex]\boxed{\sf k=44}[/tex]
Step-by-step explanation:
[tex]\sf \frac{k}{4} +3=14[/tex]
Subtract 3 from both sides.
[tex]\sf \frac{k}{4} +3-3=14-3[/tex]
[tex]\sf \frac{k}{4}=11[/tex]
Multiply both sides by 4.
[tex]\sf \frac{k}{4}(4)=11(4)[/tex]
[tex]\sf k=44[/tex]
A study regarding the relationship between age and the amount of pressure sales personnel feel in relation to their jobs revealed the following sample information. At the 0.10 significance level, is there a relationship between job pressure and age.
(Round your answers to 3 decimal places.)
Degree of Job Pressure
Age (years) Low Medium High
Less than 25 25 27 20
25 up to 40 49 53 40
40 up to 60 59 59 52
60 and older 35 42 44
H0: Age and pressure are not related. H1: Age and pressure are related.
Reject H0 if X2 > .
X2=
(Click to select)Reject Do not reject H0. Age and pressure (Click to select)areare not related.
Answers
Answer:
Reject H0
Age and pressure are related
Step-by-step explanation:
The null hypothesis is rejected or accepted on the basis of level of significance. When the p-value is greater than level of significance we fail to reject the null hypothesis and null hypothesis is then accepted. It is not necessary that all null hypothesis will be rejected at 10% level of significance. To determine the criteria for accepting or rejecting a null hypothesis we should also consider p-value. In the given scenario we reject the null hypothesis because job pressure and age are related to each other.
A 440 kg roller coaster car is going 26 m/s when it reaches the lowest point on the track. If the car started from rest at the top of a hill, how much higher was that point on the track than the lowest point? (Use g = 9.80 m/s2, and ignore friction.)
Answers
Answer:
34.49 m
Step-by-step explanation:
Use the formula height = [tex]\frac{v^{2} }{2g}[/tex]
1. Substitute in the values given
26² / 2(9.8)
2. Simplify and solve
676 / 19.6 = 34.49
Answer:
The answer is C: 34 m
helppp pleaseee!!!!!!!!!!!!
Answers
Answer:
B = 26°Step-by-step explanation:
To find Angle B we use sine
sin∅ = opposite / hypotenuse
From the question
AB is the hypotenuse
AC is the opposite
So we have
sin B = AC / AB
sin B = 4/9
B = sin-¹ 4/9
B = 26.38
B = 26° to the nearest hundredth
Hope this helps you
Answer:
[tex]\boxed{ \sf 26.39}[/tex]
Step-by-step explanation:
The triangle is a right triangle.
We can use trigonometric functions.
[tex]\sf sin(\theta )=\frac{opposite}{hypotenuse}[/tex]
[tex]\sf sin(?)=\frac{4}{9}[/tex]
[tex]\sf ?=sin^{-1}(\frac{4}{9} )[/tex]
[tex]\sf ? =26.38779996...[/tex]
This container is composed of a right circular cylinder and a right circular cone. The diameter is 20, the height of the cylinder is 9, and the slant height of the cone is 16. Find the surface area
Answers
Answer:
Total -CSA= 1068.28Step-by-step explanation:
This problem is on the mensuration of solids, a cylinder and a cone combined (a frustum)
We are required to solve for the total curve surface areas both solids
hence the curve surface area (henceforth CSA) of a cylinder is given as
[tex]CSA-cylinder=2\pi rh[/tex]
[tex]CSA-cone= \pi rl[/tex]
[tex]Total CSA= 2\pi rh+\pi rl[/tex]
Given data
diameter d= 20
radius = d/2= 20/2= 10
height of cylinder h= 9
slant height of cone l= 16
substituting our data into the expression we have
[tex]Total -CSA= 2*\pi *10*9+\pi *10*16\\\\Total -CSA= 565.56+502.72\\\Total -CSA= 1068.28[/tex]
Syrus is buying a tent with the dimensions shown below. The volume inside the tent is 4.5 m^3. Syrus isn't sure if the tent will be tall enough for him to stand inside. What is the height of the tent?
Answers
Answer: 2neters
Step-by-step explanation: I also recently did it on Khan academy
The height of the tent of the figure is H = 2 m
What is the volume of a prism?A three-dimensional solid object called a prism has two identical ends. It consists of equal cross-sections, flat faces, and identical bases. Without bases, the prism's faces are parallelograms or rectangles.
The volume of a prism is the product of its base area and height
Volume of Prism = B x h
where B = base area of prism
h = height of prism
Given data ,
Let the volume of the tent be represented as V
Now , the value of V is
V = 4.5 m³
Let the height of the prism be H
Now , the base of the triangle B = 1.5 m
And , the length of the tent L = 3 m
So , Volume of Prism = B x h
4.5 = ( 1/2 ) x 1.5 x H x 3
On simplifying , we get
4.5 = 2.25H
Divide by 2.25 on both sides , we get
H = 2 m
Hence , the height of the tent is 2 m
To learn more about volume of prism click :
https://brainly.com/question/11336446
#SPJ3
The complete question is attached below :
Syrus is buying a tent with the dimensions shown below. The volume inside the tent is 4.5 m^3. Syrus isn't sure if the tent will be tall enough for him to stand inside. What is the height of the tent?
What is 0.09% written as a decimal?
A. 0.9
B. 0.009
C. 0.0009
D. 0.09
Answers
Answer:
C. 0.0009
Step-by-step explanation:
0.09/100
= 0.0009
Answer:A
Step-by-step explanation:0.09=0.9
Katie wants to create a rectangular frame for a picture. She has 60 inches of material. If she wants the length to be 3 more than 2 times the width what is the largest possible length
Answers
Answer:
Largest possible length is 21 inches.
Step-by-step explanation:
Given:
Total material available = 60 inches
Length to be 3 more than twice of width.
To find:
Largest possible length = ?
Solution:
As it is rectangular shaped frame.
Let length = [tex]l[/tex] inches and
Width = [tex]w[/tex] inches
As per given condition:
[tex]l = 2w+3[/tex] ..... (1)
Total frame available = 60 inches.
i.e. it will be the perimeter of the rectangle.
Formula for perimeter of rectangle is given as:
[tex]P = 2 \times (Width + Length)[/tex]
Putting the given values and conditions as per equation (1):
[tex]60 = 2 \times (w+ l)\\\Rightarrow 60 = 2 \times (w+ 2w+3)\\\Rightarrow 60 = 2 \times (3w+3)\\\Rightarrow 30 = 3w+3\\\Rightarrow 3w = 27\\\Rightarrow w = 9 \ inch[/tex]
Putting in equation (1):
[tex]l = 2\times 9+3\\\Rightarrow l = 21\ inch[/tex]
So, the answer is:
Largest possible length is 21 inches.
Find the volume of the given solid region in the first octant bounded by the plane 9z+15y+15z=45 and the coordinate planes, using triple integrals.
Answers
First,
[tex]9x+15y+15z=45\implies 3x+5y+5z=15[/tex]
The volume is given by the integral (one of 6 possible combinations),
[tex]\displaystyle\int_0^5\int_0^{\frac{15-3x}5}\int_0^{\frac{15-3x-5y}5}\mathrm dz\,\mathrm dy\,\mathrm dx=\boxed{\frac{15}2}[/tex]
Which system of linear inequalities is represented by the
graph?
Answers
Answer:
The first option.
Step-by-step explanation:
y-intercept equation: y=mx+b
mx=slope
b=y-intercept
Looking at the graph, we can know that the slope is 1/3x so we can eliminate the 2nd choice. Now, we fix the second inequality into the y-intercept form which is
1st option: y>3x-2
3rd option: y>-3x+2
4th option: y>2x-2
Now, looking at the blue graph, the slope is 3x. And looking at the y-intercept, it is on -2.
So, it will be the first option!
Hope this helps, and BRAINLIEST would help me a lot!
Compute the following values when the log is defined by its principal value on the open set U equal to the plane with the positive real axis deleted.
a. log i
b. log(-1)
c. log(-1 + i)
d. i^i
e. (-i)^i
Answers
Answer:
Following are the answer to this question:
Step-by-step explanation:
The principle vale of Arg(3)
[tex]Arg(3)=-\pi+\tan^{-1} (\frac{|Y|}{|x|})[/tex]
The principle value of the [tex]\logi= \log(0+i)\ \ \ \ \ _{where} \ \ \ x=0 \ \ y=1> 0[/tex]
So, the principle value:
a)
[tex]\to \log(i)=\log |i|+i Arg(i)\\\\[/tex]
[tex]=\log \sqrt{0+1}+i \tan^{-1}(\frac{1}{0})\\\=\log 1 +i \tan^{-1}(\infty)\\\=0+i\frac{\pi}{2}\\\=i\frac{\pi}{2}[/tex]
b)
[tex]\to \log(-i)= \log(0-i ) \ \ \ x=0 \ \ \ y= -1<0\\[/tex]
Principle value:
[tex]\to \log(-i)= \log|-i|+iArg(-i) \\\\[/tex]
[tex]=\log \sqrt{0+1}+i(-\pi+\tan^{-1}(\infty))\\\\=\log1 + i(-\pi+\frac{\pi}{2})\\\\=-i\frac{\pi}{2}[/tex]
c)
[tex]\to \log(-1+i) \ \ \ \ x=-1, _{and} y=1 \ \ \ x<0 and y>0[/tex]
The principle value:
[tex]\to \log(-1+i)=\log |-1+i| + i Arg(-1+i)[/tex]
[tex]=\log \sqrt{1+1}+i(\pi+\tan^{-1}(\frac{1}{1}))\\\\=\log \sqrt{2} + i(\pi-\tan^{-1}\frac{\pi}{4})\\\\=\log \sqrt{2} + i\tan^{-1}\frac{3\pi}{4}\\\\[/tex]
d)
[tex]\to i^i=w\\\\w=e^{i\log i}[/tex]
The principle value:
[tex]\to \log i=i\frac{\pi}{2}\\\\\to w=e^{i(i \frac{\pi}{2})}\\\\=e^{-\frac{\pi}{2}}[/tex]
e)
[tex]\to (-i)^i\\\to w=(-i)^i\\\\w=e^{i \log (-i)}[/tex]
In this we calculate the principle value from b:
so, the final value is [tex]e^{\frac{\pi}{2}}[/tex]
f)
[tex]\to -1^i\\\\\to w=e^{i log(-1)}\\\\\ principle \ value: \\\\\to \log(-1)= \log |-1|+iArg(-i)[/tex]
[tex]=\log \sqrt{1} + i(\pi-\tan^{-1}\frac{0}{-1})\\\\=\log \sqrt{1} + i(\pi-0)\\\\=\log \sqrt{1} + i\pi\\\\=0+i\pi\\=i\pi[/tex]
and the principle value of w is = [tex]e^{\pi}[/tex]
g)
[tex]\to -1^{-i}\\\\\to w=e^(-i \log (-1))\\\\[/tex]
from the point f the principle value is:
[tex]\to \log(-1)= i\pi\\\to w= e^{-i(i\pi)}\\\\\to w=e^{\pi}[/tex]
h)
[tex]\to \log(-1-i)\\\\\ Here x=-1 ,<0 \ \ y=-1<0\\\\ \ principle \ value \ is:\\\\ \to \log(-1-i)=\log\sqrt{1+1}+i(-\pi+\tan^{-1}(1))[/tex]
[tex]=\log\sqrt{2}+i(-\pi+\frac{\pi}{4})\\\\=\log\sqrt{2}+i(-\frac{3\pi}{4})\\\\=\log\sqrt{2}-i\frac{3\pi}{4})\\[/tex]
There are three persons aged 60, 65 and 70 years old. The survival probabilities for these
three persons for another 5 years are 0.7.0.4 and 0.2 respectively. What is the probability
that at least two of them would survive another five years?
Answers
Answer:
Probability that at least two of them would survive another five years = 0.388
Step-by-step explanation:
We are given;
Probability of Survival of 60 years old for the next 5 years;
P(60 years old surviving) = 0.7
Thus;
Probability of 60 years old not surviving for the next 5 years;
P(60 years old not surviving) = 1 - 0.7 = 0.3
Also,given;
Probability of Survival of 65 years old for the next 5 years;
P(65 years old surviving) = 0.4
Thus;
Probability of 65 years old not surviving for the next 5 years;
P(65 years not surviving) = 1 - 0.4 = 0.6
Also,given;
Probability of Survival of 70 years old for the next 5 years;
P(70 years old surviving) = 0.2
Thus;
Probability of 70 years old not surviving for the next 5 years;
P(70 years not surviving) = 1 - 0.2 = 0.8
Probability that at least two survived is;
P(at least 2 surviving) = [P(60 surviving) x P(65 surviving) x P(70 not surviving)] + [P(60 surviving) x P(65 not surviving) x P(70 surviving)] + [P(60 not surviving) x P(65 surviving) x P(70 surviving)] + [P(60 surviving) x P(65 surviving) x P(70 surviving)]
P(at least 2 surviving) = [(0.7)(0.4)(0.8)] + [(0.7)(0.6)(0.2)] + (0.3)(0.4)(0.2) + [(0.7)(0.4)(0.2)]
P(at least 2 surviving) = 0.224 + 0.084 + 0.024 + 0.056
P(at least 2 surviving) = 0.388
A merchant had a batch of 120 face shields. If you sold 5/6 of the lot yesterday, how many protectors do you have to sell?
Answers
Answer:
Step-by-step explanation:
lot = 120 face shields
sold 5/6 of 120 =
5 × 120 ÷ 6 =
600 ÷ 6 = 100 sold of the lot.
then: 120-100 = 20
They need to sell 20 protectors.
Answer:
20 face shields.
Step-by-step explanation:
You have 120 face shields.
You sell 5/6 of them. That means that you still have to sell 1 - 5/6 = 1/6 of the lot.
120 * (1/6) = 20 * 1 = 20 face shields to sell.
Hope this helps!
anyone know how to do this. im hella lost right now
Answers
Answer:
a=6
b=5.5
Step-by-step explanation:
not very sure but..
since 8X2=16,
a=3X2
b=11/2
Suppose that a single die with 9 sides (numbered 1, 2, 3, ... , 9) is rolled twice. What is the probability that the sum of the two rolls equals 3
Answers
Answer:
2/81Step-by-step explanation:
Probability is defines as the likelihood or chance that an event will occur.
Probability = expected outcome of event/total outcome.
Since a single die with 9 sides was rolled, the total event outcome will be 9*9 = 81
Expected outcome will be the event that the sum of the two rolls equals 3. The possible outcomes are {(1,2), (2,1)}. The expected outcome is 2
Probability that the sum of the two rolls equals 3 = 2/81
The probability that the sum of the two rolls equals 3 is [tex]\dfrac{2}{81}[/tex].
Important information:
A single die with 9 sides is rolled twice.We need to find the probability that the sum of the two rolls equals 3.
Probability:If a die with 9 sides is rolled twice, then the number of total possible outcomes is:
[tex]9\times 9=81[/tex]
The sum of the two rolls equals 3, if we get 1, 2 and 2, 1. It means the number of favorable outcomes is 2.
[tex]P=\dfrac{\text{Favorable outcomes}}{\text{Total outcomes}}[/tex]
[tex]P=\dfrac{2}{81}[/tex]
Therefore, the probability that the sum of the two rolls equals 3 is [tex]\dfrac{2}{81}[/tex].
Find out more about 'Probability' here:
https://brainly.com/question/6778390
In a poll conducted by the Gallup organization in April 2013, 48% of a random sample of 1022 adults in the U.S. responded that they felt that economic growth is more important than protecting the environment. We can use this information to calculate a 95% confidence interval for the proportion of all U.S. adults in April 2013 who felt that economic growth is more important than protecting the environment. Make sure to include all steps.
Answers
Answer:
The 95% confidence interval is [tex]0.449 < p < 0.48 + 0.511[/tex]
Step-by-step explanation:
From the question we are told that
The sample proportion is [tex]\r p = 0.48[/tex]
The sample size is [tex]n = 1022[/tex]
Given that the confidence level is 95% then the level of significance is mathematically evaluated as
[tex]\alpha = 100 - 95[/tex]
[tex]\alpha = 5 \%[/tex]
[tex]\alpha = 0.05[/tex]
Next we obtain the critical value of [tex]\frac{\alpha }{2}[/tex] from the z-table , the value is
[tex]Z_{\frac{\alpha }{2} } =Z_{\frac{0.05 }{2} }= 1.96[/tex]
The reason we are obtaining critical value of [tex]\frac{\alpha }{2}[/tex] instead of [tex]\alpha[/tex] is because
[tex]\alpha[/tex] represents the area under the normal curve where the confidence level interval ( [tex]1-\alpha[/tex] ) did not cover which include both the left and right tail while [tex]\frac{\alpha }{2}[/tex] is just the area of one tail which what we required to calculate the margin of error
NOTE: We can also obtain the value using critical value calculator (math dot armstrong dot edu)
Generally the margin of error is mathematically represented as
[tex]E = Z_{\frac{\alpha }{2} } * \sqrt{\frac{\r p (1- \r p )}{n} }[/tex]
substituting values
[tex]E = 1.96* \sqrt{\frac{0.48 (1- 0.48 )}{1022} }[/tex]
[tex]E = 0.03063[/tex]
The 95% confidence interval is mathematically represented as
[tex]\r p - E < p < \r p + E[/tex]
substituting values
[tex]0.48 - 0.03063 < p < 0.48 + 0.03063[/tex]
[tex]0.449 < p < 0.48 + 0.511[/tex]
One number is 26 more than another. Their product is -169.
Answers
One number = x
One number more 26 = x + 26
Their product is -169
x . (x + 26) = -169
x² + 26x = -169
x² + 26x + 169 = 0
x² + 2.13.x + 13² = 0
It can be written by
(x + 13)² since we know that (x + 13)² = x² + 2.x.13 + 13²
So
(x + 13)² = 0
x + 13 = 0
x = -13
Our number is -13
Step-by-step explanation:
Here, according to the question,
let one number be x and another number be x +26 as given in question that the another number is more than 26.
And their product is given as -169.
now, as per the condition of question,
x × (x+26)= -169
or, x^2+26x= -169
or, x^2+26x+169=0
or, (x+13)^2=0
or, (x+13)=0 (root under 0= 0)
or, x=-13.
Therefore, thevalue of x is -13.
And the value of (x+26) is (-13+26)=13.
Checking, 13×-13=-169.
Therefore, the 2 numbers are -13 and 13.
hope it helps...
Which ordered pair is a solution of the equation? y=3x+5 A:(2,11) B:(3,13) C: Neither D: Both
Answers
Answer:
A: (2, 11).
Step-by-step explanation:
For an ordered pair to be a solution of an equation, the ordered pair must "fit".
A: (2, 11).
11 = 3(2) + 5
11 = 6 + 5
11 = 11
So, (2, 11) is a solution.
B: (3, 13).
13 = 3(3) + 5
13 = 9 + 5
13 = 14
Since 13 is not the same thing as 14, (3, 13) is not a solution.
Since A works but B doesn't, choices C and D are both eliminated. A is your answer.
Hope this helps!