Answers
Answer:
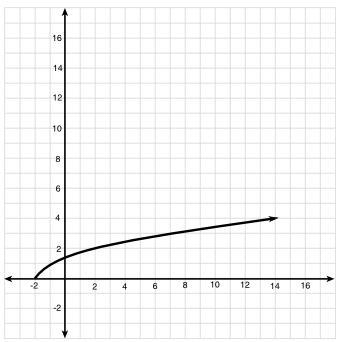
The function graphed below is [tex]x = y^{2} - 2[/tex] or [tex]y = \pm \sqrt{x+2}[/tex].
Step-by-step explanation:
The graph represents a second order polynomial function (a parabola), whose axis of symmetry is the x-axis and whose form is presented as follows:
[tex]x - h = C\cdot (y-k)^{2}[/tex]
Where:
[tex]x[/tex], [tex]y[/tex] - Dependent and independent variable, dimensionless.
[tex]h[/tex], [tex]k[/tex] - Horizontal and vertical components of the vertex, dimensionless.
[tex]C[/tex] - Vertex constant, dimensionless. If [tex]C > 0[/tex], then vertex is an absolute minimum, otherwise it is an absolute maximum.
After a quick observation, the following conclusions are done:
1) Vertex is an absolute minimum ([tex]C > 0[/tex]) and located at (-2, 0).
2) Parabola pass through (2, 2).
Then, the value of the vertex constant is obtained after replacing all known values on expression prior algebraic handling: ([tex]x = 2[/tex], [tex]y = 2[/tex], [tex]h = -2[/tex], [tex]k = 0[/tex])
[tex]2+2 = C\cdot (2-0)^{2}[/tex]
[tex]4 = 4\cdot C[/tex]
[tex]C = 1[/tex]
The function is:
[tex]x = -2 + 1\cdot y^{2}[/tex]
[tex]x = y^{2}-2[/tex]
The inverse function of this expression is [tex]y = \pm \sqrt{x+2}[/tex]
The function graphed below is [tex]x = y^{2} - 2[/tex] or [tex]y = \pm \sqrt{x+2}[/tex].
Related Questions
HELPPPP The equation 2x = 3y – 5 when written in slope-intercept form is: y = 2x – 5. y = -2x + 5. y = 2x + 5. None of these choices are correct.
Answers
Answer:
Y= 2/3x +(5/3)
Step-by-step explanation:
First, have to get Y alone on one side 3y=2x+5
Second, have to get read of the 3 with the Y so divide each side by three.
a kilobyte is 2^10 bytes and a megabyte is 2^20 . how many kilobytes are in a megabyte
Answers
Answer:
1024
Step-by-step explanation:
so first you would do 2^10 and 2^20
2^10 = 1024
2^20 = 1048576
then you would just divide 1048576 by 1024
1048576 / 1024 = 1024
1/6.43 +2/3.56 +1/8.51 use reciprocal table.Correct answer only
Answers
Answer:
0.8348Step-by-step explanation:
Given the expression 1/6.43 +2/3.56 +1/8.51, If 'a' is a number, the reciprocal of such number is 1/a. According to the question, the reciprocal of 6.43, 3.56 and 8.51 are 1/6.43 and 1/3.56 and 1/8.51 respectively.
1/6.43 = 0.1555
2/3.56 = 2 * 1/3.56
= 2 * 0.2809
= 0.5618
1/8.51 = 0.1175
Taking the sum of the reciprocals;
1/6.43 +2/3.56 +1/8.51 = 0.1555 + 0.5618 + 0.1175
1/6.43 +2/3.56 +1/8.51 = 0.8348
Hence, the sum of 1/6.43, 2/3.56 and 1/8.51 is 0.8348
Please answer it now in two minutes
Answers
Answer:
3√6
Step-by-step explanation:
tan60=opp/adj
opp(d)=tan60*3√2=√3*3√2=3√6
Plz write this on paper help me and send it❤️
Answers
Answer:
1. [tex]27^{\frac{2}{3} } =9[/tex]
2. [tex]\sqrt{36^{3} } =216[/tex]
3. [tex](-243)^{\frac{3}{5} } =-27[/tex]
4. [tex]40^{\frac{2}{3}}=4\sqrt[3]{25} =4325[/tex]
5. Step 4: [tex](\frac{343}{27}) ^{-1} =\frac{27}{343}[/tex]
6. [tex]D. -72cd^{7}[/tex]
Step-by-step explanation:
Use the following properties:
[tex]a^{\frac{x}{y} } =\sqrt[x]{a^{y} }[/tex]
[tex]\sqrt[n]{ab} =\sqrt[n]{a} \sqrt[n]{b}[/tex]
[tex]a^{-n} =\frac{1}{a^{n} }[/tex]
[tex](xy)^{z} =x^{z} y^{z} \\\\[/tex]
[tex](x^{y}) ^{z} =x^{yz}[/tex]
[tex]x^{y} x^{z} =x^{y+z}[/tex]
So:
1. [tex]27^{\frac{2}{3} } =\sqrt[3]{27^{2}} =\sqrt[3]{729} }=9[/tex]
2. [tex]\sqrt{36^{3} } =\sqrt{36*36*36} =\sqrt{36} \sqrt{36} \sqrt{36} =6*6*6=216[/tex]
3. [tex](-243)^{\frac{3}{5} } =\sqrt[5]{-243^{3} } =\sqrt[5]{-14348907} =-27[/tex]
4. [tex]40^{\frac{2}{3}}=\sqrt[3]{40^{2} } =\sqrt[3]{2^{6} 5^{2} } =\sqrt[3]{2^{6} } \sqrt[3]{5^{2} } =2^{\frac{6}{3} } 5^{\frac{2}{3} } =4 *5^{\frac{2}{3} } =4\sqrt[3]{5^{2} } =4\sqrt[3]{25}=4325[/tex]
5. [tex](\frac{343}{27}) ^{-1} =\frac{1}{\frac{343}{27} } =\frac{27}{343}[/tex]
6.
[tex](-8c^{9} d^{-3} )^{\frac{1}{3} } *(6c^{-1}d^{4})^{2} =\sqrt[3]{-8} c^{3} d^{-1} 36c^{-2} d^{8} \\\\-2c^{3} d^{-1} 36c^{-2} d^{8}=-72cd^{7}[/tex]
BC is parallel to DE.
AB= X, AD=5, AC=X+1 and AE=7. The value of X is?
A: 0.5
B: 1.5
C: 2.5
D: 3.5
Answers
Answer:
x= 2.5
Step-by-step explanation:
We can use ratios to solve
AB AD
------- = ----------
AC AE
X 5
------- = ----------
x+1 7
Using cross products
7x = 5(x+1)
Distribute
7x = 5x+5
subtract 5x
7x-5x = 5x-5x+5
2x= 5
Divide by 2
2x/2 = 5/2
x = 2.5
work out the shaded area.
plzzzz
Answers
Answer:
Shaded area: 70cm^2
Step-by-step explanation:
Whole=120cm^2
White Square=
10-2.5-2.5=5
12-1-1=10
5✖️10=50cm^2
Whole-white=70cm^2
You can buy 5 cans for green beans at the village market for $2.80. You can buy 10 of the same cans of beans at Sam's club for $4.90. Which place is the better to buy
Answers
Answer:
The unit price at the village market is 2.80 / 5 = 0.56 and the unit price at Sam's Club is 4.90 / 10 = 0.49. Since 0.49 < 0.56, the answer is Sam's Club.
Answer: Sam's club
Step-by-step explanation:
Because 10/2 = 5, at Sam's club you get twice the beans. Thus, simply multiply 2.8*2 = 5.60. Because $5.60>$4.90, the village market is the worse place to buy.
Simplify the expression 3^-8× 34.
Answers
Answer:
= [tex]\frac{34}{6561}[/tex]
Step-by-step explanation:
[tex]= 3^{-8}\times \:34\\= 34\times \frac{1}{3^{8} } \\= \frac{1\times \:34}{3^{8} } \\= \frac{34}{3^{8} } \\= \frac{34}{6561}[/tex]
Answer:
1/81
Step-by-step explanation:
A football team lost 5 yards on one play and gained 12 yards on the next play. Find the overall change in field position.
Answers
Answer:
Equation: -5 + 12
Overall change: 7 yards
Step-by-step explanation:
In the problem, it says "lost 5 yards". "Lost" is another way of saying subtraction or negative. Therefore, our starting number is -5.
The problem also says "gained 12 yards". "Gained" is another was of saying addition or positive. Therefore, our second number is positive 12.
Together, these two numbers look like this: -5 + 12. To add them, go 12 to the right of -5 if on a number line. That would be like this: -5, -4, -3, -2, -1, 0, etc until you get to 7 which should be 12 more than -5.
Therefore, the answer is 7 yards.
what's the value? A.-20 B.-4 C.4 D.20
Answers
Answer:
-4Option B is the correct option.
Step-by-step explanation:
[tex] {(4 - 2)}^{3} - 3 \times 4[/tex]
Subtract the numbers
[tex] = {(2)}^{3 } - 3 \times 4[/tex]
Multiply the numbers
[tex] = {(2)}^{3} - 12[/tex]
Evaluate the power
[tex] = 8 - 12[/tex]
Calculate the difference
[tex] = - 4[/tex]
Hope this helps..
Best regards!!
Answer:
[tex]\boxed{-4}[/tex]
Step-by-step explanation:
[tex](4-2)^3-3 \times 4[/tex]
Brackets or parenthesis are to be evaluated first. Subtract the numbers in the brackets.
[tex](2)^3-3 \times 4[/tex]
Evaluate the power or exponent.
[tex]8-3 \times 4[/tex]
Multiply the numbers.
[tex]8-12[/tex]
Finally, subtract the numbers.
[tex]=-4[/tex]
He Perimeter of a
regular decagon is 328cm
stake the length of one of its
sides
Answers
Answer:
32.8 cm
Step-by-step explanation:
decagons have 10 sides, so 328/10=32.8
Answer:
32.8 cm
Step-by-step explanation:
A regular decagon has 10 equal sides.
The perimeter of the decagon is 328 centimeters. The perimeter is the measure of all 10 sides added together. Since this is a regular decagon, all 10 sides are equal. Therefore, we can divide 328 by 10.
328 / 10
32.8
Add units, in this case, centimeters or cm.
32.8 cm
Each side of the decagon is 32.8 centimeters.
HELP!! this is due today
Answers
Answer:
1
Step-by-step explanation:
If y=x, than the only way
y=rx can be possible is if r=1
Hope this helps!
Have a good day! :)
Answer:
1
Step-by-step explanation:
y = rx
Use any set of x and y-coordinates in the equation and solve for r.
For example, use (5.8, 5.8).
5.8 = r(5.8)
Divide both sides by 5.8:
r = 1
Answer: r = 1
What is the slope of the graph?
Answers
Answer:
-2
Step-by-step explanation:
The slope formula is
m = ( y-2-y1)/(x2-x1)
Using two points on the line (0,4) and (2,0)
m = ( 0-4)/(2-0)
= -4/2
=-2
Answer:
-2
Step-by-step explanation:
Slope is change in y over change in x
the change in y is -2 and the change in x is 1 so you do -2/1 and that as a whole number is -2.
The summer has ended and it's time to drain the swimming pool. 20 minutes after pulling the plug, there is still 45 000L of water in the pool. The pool is empty after 70 minutes. Calculate the rate that the water is draining out of the pool. b) Calculate how much water was in the pool initially. c) Write an equation for this relationship. d) Use your equation to calculate how much water is in the pool at 62 minutes.
Answers
Answer:
a) -900 L/min
b) 63000 L
c) -900t +63000
d) 7200 L
Step-by-step explanation:
a) You are given two points on the curve of volume vs. time:
(t, V) = (20, 45000) and (70, 0)
The rate of change of volume
= ΔV/Δt = (0 -45000)/(70 -20) = -45000/50 = -900 liters per minute
b) In the first 20 minutes, the change in volume was
(20 min)(-900 L/min) = -18000 L
So, the initial volume was
initial volume - 18000 = 45000
initial volume = 63,000 liters
c) Since we have the slope and the intercept, we can write the equation in slope-intercept form as
V= -900t +63000.
d) now putting the number in the equation and do the arithmetic.
When t=62, the amount remaining is
= -900(62) +63000 = -55800 +63000 = 7200
Thus, 7200 L remain after 62 minutes.
Examine the system of equations. –2x + 3y = 6 –4x + 6y = 12 Answer the questions to determine the number of solutions to the system of equations. What is the slope of the first line? What is the slope of the second line? What is the y-intercept of the first line? What is the y-intercept of the second line? How many solutions does the system have?
Answers
Answer:
Examine the system of equations.
–2x + 3y = 6
–4x + 6y = 12
Answer the questions to determine the number of solutions to the system of equations.
What is the slope of the first line?
✔ 2/3
What is the slope of the second line?
✔ 2/3
What is the y-intercept of the first line?
✔ 2
What is the y-intercept of the second line?
✔ 2
How many solutions does the system have?
✔ infinitely many
The equations are a multiple of the other, therefore, by the multiplicative
property of equality, the equations are equivalent.
Response:
The slope and y-intercept of the first equation are [tex]\underline{\dfrac{2}{3} \ and \ 2}[/tex] respectivelyThe slope and y-intercept of the second equation are [tex]\underline{\dfrac{2}{3} \, and \, 2}[/tex]The system of equations have infinitely many solutions.Methods used to obtain the above response.The given system of equations are;
-2·x + 3·y = 6
-4·x + 6·y = 12
Required:
The slope of the first line.
Solution:
The slope of the first line is given by the coefficient of x when the equation is expressed in the form; y = m·x + c.
Therefore, from -2·x + 3·y = 6, we have;
3·y = 2·x + 6
[tex]y = \dfrac{2}{3} \cdot x + \dfrac{6}{3} = \dfrac{2}{3} \cdot x + 2[/tex]
[tex]y =\dfrac{2}{3} \cdot x + 2[/tex]
[tex]\underline{The \ slope \ of \ the \ first \ equation \ is \ \dfrac{2}{3}}[/tex]
Required:
The slope of the second line;
Solution:
The equation of the second line, -4·x + 6·y = 12, can be expressed in the form;
[tex]y =\dfrac{4}{6} \cdot x + \dfrac{12}{6} = \dfrac{2}{3} \cdot x + 2[/tex]
[tex]y = \mathbf{\dfrac{2}{3} \cdot x + 2}[/tex]
[tex]\underline{The \ slope \ of \ the \ second \ equation \ is \ therefore \ \dfrac{2}{3}}[/tex]
The y-intercept of the first line = 2The y-intercept of the second line = 2Given that the equation have the same slope and the same y-intercept, the equations are equations of the same line, therefore;
The equations have an infinite number of solutionsLearn more about the solutions of a system of equations here:
https://brainly.com/question/15356519
An algebraic expression for the perimeter of a rectangle with a length of 4x and a width of 3x
Answers
P = 2l + 2w
Then multiply 2 times each term:
So you have 2(4x)= 8x
Then 2(3x)= 6x
Answer: the algebraic expression for the perimeter of the rectangle is 8x+6x
URGENT
What else would need to be congruent to show that AABC= ADEF by the
AAS theorem?
Answers
Answer:
AC = EF
Step-by-step explanation:
ABC = DEF
You would need to know that AC = EF
In the first place, using deduction we know that we dont need another angle. We also know that BC does not equal DF by looking at the angles on the triangles.
The solution is : ∠C ≅ ∠F is congruent to show that ΔABC ≅ ΔDEF, else would need to be congruent to show that AABC= ADEF by the AAS theorem.
What is AAS theorem?The angle-angle-side theorem, or AAS, tells us that if two angles and a non-included side of one triangle are congruent to two angles and a non-included side of another triangle, then the triangles are congruent.
here, we have,
to find congruency in a triangle:
ΔABC ≅ ΔDEF
Therefore,
AAS congruence rule or theorem states that if two angles of a triangle with a non-included side are equal to the corresponding angles and non-included side of the other triangle, they are considered to be congruent.
Therefore,
∠C ≅ ∠F
Hence, The solution is : ∠C ≅ ∠F is congruent to show that ΔABC ≅ ΔDEF, else would need to be congruent to show that AABC= ADEF by the AAS theorem.
learn more on AAS here:
brainly.com/question/2699309
#SPJ7
Pls solve ASAP!! Review the attachment and solve. Pls hurry!
Answers
Answer:
A. 3
Step-by-step explanation:
ΔDEC is bigger than ΔABC by 5. For the hypotenuse, 25 is 5 times bigger than 5.
So, side DE on ΔDEC has to be 5 times bigger than side AB on ΔABC.
If side AB equals 3, side DE equals 18 - 3, which is 15.
15 is five times bigger than 3, so the answer is A. 3.
Hope that helps.
does not
Ether.
1-36. If y varies directly with x and y is 12 when x is 4, then
what is y when x is 8?
what is when x is 3?
what is x when y is 6?
a.
b.
n.
C.
Answers
Answer:
Step-by-step explanation:
Hello!
Y varies directly with X, meaning that every time X increases/ decreases, the value of Y is modified.
If Y=12 when X=4 then you can say that Y varies 3 times every time X varies 1 unit
12= 4*z
z=12/4= 3
So Y= 3x
With this in mind:
1) x= 8
Y= 3*8= 24
2) x= 3
Y= 3*3= 9
3) Y= 6
Y= 3x
x=Y/3= 6/3= 1
I hope this helps!
Greg goes fishing every day for a week. On the first day he catches seven fish and each
day he catches three more than the previous day. How many fish did he catch in total?
Answers
so first day and so on
7, 10, 13,....
as you can see it's an arithmetic progression
so sum for nth term= n/2 { 2a + (n-1) d}
it's the sum of the 7th term
so
7/2 { 7 ×2 + ( 7-1) 3}
7/2 × 32
7× 16
112 fishes
Answer:
I think the answer is 25
Step-by-step explanation:
7+3+3+3+3+3+3 becuase a week is seven days and the numbers there is seven ,and you plus the 7 with the remaining six days which are 3 each day,my answer was now 25 .please if you know this answer is wrong please tell everyone the correct oneBill needs to edge his yard with the dimensions in the shape below. What distance will he have walked after completing his edging? Round your answer to one decimal place. Do not include units in your answer.
Answers
Answer:
37.8 m
Step-by-step explanation:
The computation of the distance is shown below:
In triangle ADE
[tex]AD^2 = AE^2 + DE^2 \\\\ AD^2 = 5^2 + 3^2 \\\\ AD^2 = 34[/tex]
AD = 5.8
Now the distance walked after completing his edging is
Distance = AD + AB + BC + CD
= 5.8 + 12 + 5 + 15
= 37.8 m
We simply added these four sides so that the correct distance could arrive
Hence, the distance walked after completing his edging is 37.7
Which of the following formulas would find the lateral area of a right cylinder
with height equal to hand ras the radius?
O A. LA = 2πr2
O B. LA = 2πr
O C. LA = 2πrh
O D. LA = 2πr2
Answers
Answer:
C - LA = 2πrh
Step-by-step explanation:
Lateral surface area of right cylinder = 2 * π * radius * height
Dora bought a bottle of nail polish that was marked down by 20 percent from its original price of $4.50. Including a 9 percent sales tax, what is the final cost of the bottle of nail polish?
Answers
Answer:
Hey there!
Marked down by 20 percent is equal to 80 percent of the original value.
4.5(0.8)=3.6
9 percent sales tax
3.6(1.09)=3.92
Hope this helps :)
Answer:
$3.92
Step-by-step explanation:
I took the test
En la figura los segmentos ED y AC son paralelos selecciona los triangulos q son 1)Triangulo ABE 2)Triangulo BCD 3) Triangulo BDE
Answers
Respuesta:
Los 3 triángulos son semejantes.
Explicación paso a paso:
En estos casos nos dan a conocer los ángulos de los triángulos, por lo tanto el criterios de semejanza se reduce si más de dos de sus ángulos internos son iguales.
Por lo tanto, sabemos que en los triángulos ABE y BCD presentan los mismos ángulos, 80°, 40° y 60° por lo que podemos afirmar que ambos triángulos son semejantes.
Ahora bien, para el triangulo BDE, podemos conocer solo un angulo del que es de 80°, pero el resto sería desconocido, lo que quiere decir que no podríamos determinar si es semejante con los otros, pero por medio de los ángulos externos determinamos que si corresponde también a 60° y 40°, por lo tanto, los 3 triángulos son semejantes.
can someone please help me
Answers
Answer:
3x^2 + 3/2 x -9
Step-by-step explanation:
f(x) = x/2 -3
g(x) =3x^2 +x -6
(f+g) (x) = x/2 -3 + 3x^2 +x -6
Combine like terms
= 3x^2 + x/2 +x -3-6
= 3x^2 + 3/2 x -9
solve for x, if a solution is extraneous identify in the final answer. thx :)
Answers
Answer:
x = 6 and x = 11.
Step-by-step explanation:
sqrt(x - 2) + 8 = x
sqrt(x - 2) = x - 8
(sqrt(x - 2))^2 = (x - 8)^2
x - 2 = x^2 - 16x + 64
x^2 - 16x + 64 = x - 2
x^2 - 17x + 66 = 0
We can use the discriminant to find whether there are solutions to the equation.
b^2 - 4ac; where a = 1, b = -17, and c = 66.
(-17)^2 - 4 * 1 * 66
= 289 - 264
= 25
Since the discriminant is positive, we know there are two valid solutions to the equation.
x^2 - 17x + 66 = 0
(x - 6)(x - 11) = 0
The solutions are when x - 6 = 0 and x - 11 = 0.
x - 6 = 0
x = 6
x - 11 = 0
x = 11
Hope this helps!
Answer:
x=11 solution
x=6 extraneous
Step-by-step explanation:
sqrt( x-2) + 8 = x
Subtract x from each side
sqrt(x-2) = x-8
Square each side
(sqrt(x-2))^2 = (x-8) ^2
x-2 = x^2 -8x-8x+64
x-2 = x^2 -16x+64
Subtract ( x-2) from each side
0 = x^2 -17x +66
Factor
0 = (x-6) ( x-11)
Using the zero product property
x=6 x=11
Checking the solutions
x=6
sqrt( 6-2) + 8 = 6
sqrt(4) +8 = 6
2 +8 = 6
False not a solution
x=11
sqrt( 11-2) + 8 = 11
sqrt(9) +8 =11
3 +8 = 11
solution
At the U.S. Open Tennis Championship a statistician keeps track of every serve that a player hits during the tournament. The statistician reported that the mean serve speed of a particular player was 103 miles per hour (mph) and the standard deviation of the serve speeds was 11 mph.Assume that the statistician also gave us the information that the distribution of serve speeds was mound-shaped and symmetric. What percentage of the player's serves were between 115 mph and 145 mph?
A) approximately 16%
B) at most 34%
C) at most 2.5%
D) at most 13.5%
Answers
Answer:
D
Step-by-step explanation:
What we need to do here is to calculate the required probability and convert to percentage
Firstly, we start by calculating the z-scores of the two boundary limits
Mathematically;
z-score = (x-mean)/SD
Form the question, we can see that the mean is 103 and the standard deviation is 11
so for 115, z-score would be
z-score = (115-103)/11 = 1.1
For 145, z-score would be
(145-103)/11 = 3.8
So the probability we want to calculate would be;
P(1.1<z<3.8)
We use the standard normal table for this
Mathematically;
P(1.1<z<3.8) = P(z<3.8) - P(z<1.1) = 0.13559
which to percentage is 13.559 %
The closest answer here is D
graph the circle x2 + y2 - 12x + 6y +36 =0
Answers
x^2+y^2-12x+6y+36=0
Top Point: (6,0)
Left Point: (3,-3)
Right Point: (9,-3)
Bottom Point: (6,-6)
Answer:
[tex] x^2 +y^2 -12x +6y +36 =0[/tex]
And we can complete the squares like this:
[tex] (x^2 -12x +6^2) + (y^2 +6y +3^2) = -36 +6^2 +3^2[/tex]
And we got:
[tex] (x-6)^2 + (y+3)^2 = 9[/tex]
And we have a circle with radius r =3 and the vertex would be;
[tex] V= (6,-3) [/tex]
The graph is on the figure attached.
Step-by-step explanation:
For this case we have the following expression:
[tex] x^2 +y^2 -12x +6y +36 =0[/tex]
And we can complete the squares like this:
[tex] (x^2 -12x +6^2) + (y^2 +6y +3^2) = -36 +6^2 +3^2[/tex]
And we got:
[tex] (x-6)^2 + (y+3)^2 = 9[/tex]
And we have a circle with radius r =3 and the vertex would be;
[tex] V= (6,-3) [/tex]
The graph is on the figure attached.
Explain how to solve the equation |2x-3| = x^2 graphically. Using a graphing calculator to find all real number solutions to the equation.
Answers
Answer:
x = -3 , x = 1
Step-by-step explanation:
Hello,
you need to draw the graph of the two functions and then find the intersection points.
please see below
So the solution is the two points A and B
(-3,9) and (1,1)
Hope this helps