please help me to understand how this problem was solved. if you aren't going to explain don't even bother. no trolling :0

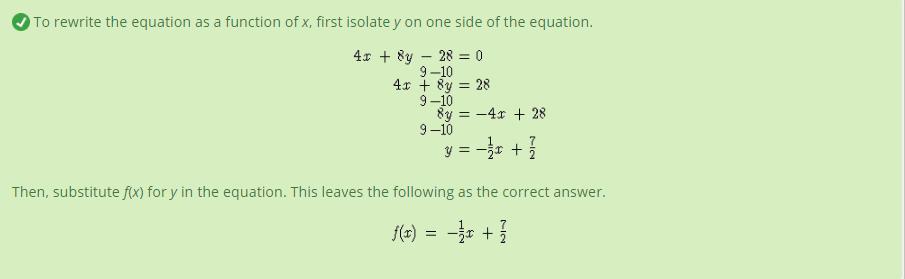
Answer:

[tex]\large \boxed{\sf \ \ \text{The maximum profit is \$94 per day.} \ \ }[/tex]

Step-by-step explanation:

Hello,

The coefficient in [tex]x^2[/tex] is negative.

So, there is a maximum at the vertex point which is

[tex]x=-\dfrac{b}{2a}==\dfrac{-6}{-0.2}=\dfrac{6}{0.2}=30[/tex]

And then the maximum is f(30)=

[tex]-0.1\cdot 30^2+6\cdot 30 +4=-90 +180+4=94[/tex]

So the maximum profit is 94 $ per day.

Hope this helps.

Do not hesitate if you need further explanation.

Thank you

Answer:

a. 30 meters per second

b. -10 meters per second

Step-by-step explanation:

a. Average rate of change for the height from 0 to 6.6 secs can be calculated using the formula, [tex] m = \frac{H(b) - H(a)}{b - a} [/tex]

Thus,

Where,

[tex] a = 0, H(0) = 0 [/tex]

[tex] b = 6.6, H(6.6) = 198 [/tex]

Plug in the values into the formula:

[tex] m = \frac{198 - 0}{6.6 - 0} [/tex]

[tex] m = \frac{198}{6.6} [/tex]

[tex] m = 30 [/tex]

b. Average rate of change for the height from 8.8 to 13.2 secs = tex] m = \frac{H(b) - H(a)}{b - a} [/tex]

Where,

[tex] a = 8.8, H(8.8) = 44 [/tex]

[tex] b = 13.2, H(13.2) = 0 [/tex]

Plug in the values:

[tex] m = \frac{0 - 44}{13.2 - 8.8} [/tex]

[tex] m = \frac{-44}{4.4} [/tex]

[tex] m = -10 [/tex]

Step-by-step explanation:

Hello!!!

Given, VXW is a Right angled triangle where WV =4 and XV =5.

now, by taking reference angle as angle W, and using tangent we get;

p=5

b=4

again,

tan thita =p/b

tan thita = 5/4

so, tan thita =1.25.

now, to find angle W, we should do tan thita inverse;

or, (tan thita)-1= tan thita-1(1.25)

or, (tan thita) -1 =51.3401°.

Now, by rounding off we get,

tan thita (angle W )= 51°.

Hope it helps....

Answer:

$3.60

Step-by-step explanation:

Convert the percentage to a decimal.

2% = 0.02

Multiply the cost of the dress by the decimal to find the sales tax.

$180 × 0.02 = $3.60

The sales tax $3.60.

Answer:

3.60

Step-by-step explanation:

sales tax = cost * tax rate

                = 180 * 2%

                 = 180 * .02

                 =3.60

Answer:

I believe the median is 6.5

Step-by-step explanation:

Answer:

a

Step-by-step explanation:

Since the graph intersects the x-axis at 2 points, it has 2 solutions which means that the discriminant is greater than 0. The only option that satisfies this is 10.

Answer:

10  option a)

Step-by-step explanation:

The discriminant has to be a number greater than zero, since we clearly see two solutions (crossings of the x axis) of the curve. So, the only option larger than zero among the possible answers is 10 (option a)

━━━━━━━☆☆━━━━━━━

▹ Answer

You can use a graphing calculator. Attached is a picture of it graphed.

Hope this helps!

CloutAnswers ❁

Brainliest is greatly appreciated!

━━━━━━━☆☆━━━━━━━

Answer:

288

Step-by-step explanation:

Answer:

[tex]V=72\pi ft^3[/tex]

Step-by-step explanation:

Recall the formula for the volume of a cone:

[tex]V=\frac{1}{3}\pi r^2h[/tex]

Where r is the radius and h is the vertical height.

We know that the diameter is 12ft. This means that radius must be 6ft.

And we are given that the vertical height is 6ft.

Plug in the numbers:

[tex]V=\frac{1}{3}\pi (6)^2(6)\\V=2(36)\pi\\V=72\pi ft^3[/tex]

Answer:

0.60

Step-by-step explanation:

find the probability it is a 2:

0.40 / 1 = 0.4 or 40%

find the probability it isn't a 2:

1 - 0.4 = 0.6

Answer:

A. 0.60

Step-by-step explanation:

I did geometry last year. My teacher assigned it to us.

Hope this helps :)

Answer:

SOLUTION SET ={a/a≥20}

Step-by-step explanation:

[tex]\frac{2a}{5}-2\geq\frac{a}{4}+1[/tex]

[tex]adding 2 on both sides[/tex]

[tex]\frac{2a}{5}-2+2\geq \frac{a}{4}+1+2[/tex]

[tex]now subtracting \frac{a}{4} on both sides[/tex]

[tex]\frac{2a}{5}-\frac{a}{4}\geq 3[/tex]

[tex]takig LCM as 20\\\frac{8a}{20}-\frac{5a}{20}\geq 3[/tex]

[tex]\frac{3a}{20}\geq 3[/tex]

[tex]by cross-multiplication[/tex]

3a≥3×20

3a≥60

dividing 3 on both sides

3a/3≥60/3

a≥20

SOLUTION SET ={a/a≥20} is the answer

i hope this will help you :)

Answer:

Sum of two rational numbers-

-10 = -5+-5

0= -5+5

15= 10+5

Step-by-step explanation:

Answer:

6 i

Step-by-step explanation:

The imaginary number "6 i" when squared gives :[tex](6\,i)^2=36\,(i)^2=36 (-1) = -36[/tex]

Answer:

Step-by-step explanation:

[tex]\\ \sqrt{-36 }=\sqrt{36 \times -1} =\sqrt{36 \times \iota^2}=\pm 6 \iota\\so~ 0+6 \iota\\and~0-6 \iota[/tex]

Answer:

Ram therefore has more amount in his account at the end of the month, and the balances in their bank accounts at the end of the month are arranged in ascending order, i.e. from the smallest to the largest, as follows:

Rahul – Debits AED 200; Rohit – Credits AED 200; and Ram – Credits AED 500.

Step-by-step explanation:

In banking and finance, a credit transaction on a bank account indicates that an additional amount of money has been added to the bank account and the balance has increased. This gives a positive balance in the account

On the other hand, a debit transaction on a bank account indicates that an amount of money has been deducted or withdrawn from the bank account and the balance has therefore reduced. This gives a negative balance in the account.

Based on the above, we have:

a. Ram – Credits AED 500 on 12th May 2020

Since there is no any other credit or debit transaction during the month, this implies that Ram still has Credits AED 500 in his account at the end of the month.

The Credits AED 500 indicates that Ram has a positive balance of AED 500 in his account at the end of the month.

b. Rahul – Debits AED 700 on 12th May 2020 and Credits AED 500 on 15th May 2020.

The balance in the account of Rahul gives Debits of AED 200 as follows:

Debits AED 700 - Credits AED 500 = Debits AED 200

The Debits AED 200 indicates that Rahul has a negative balance of AED 200 in his account at the end of the month.

c. Rohit – Credits AED 700 on 12th May 2002 and Debits AED 500 on 15th May 2020.

The balance in the account of Rohit gives Credits of AED 200 as follows:

Credits AED 700 - Dedits AED 500 = Credits AED 200

The Credits AED 200 indicates that Rohit has a positive balance of AED 200 in his account at the end of the month.

Conclusion

Arrangement of numbers or amounts of money in ascending order implies that they are arranged from the smallest to the largest number or amount.

Since Credits implies positive amount and Debits implies negative amount, Ram therefore has more amount in his account at the end of the month, and the balances in their bank accounts at the end of the month are arranged in ascending order, i.e. from the smallest to the largest, as follows:

Rahul – Debits AED 200; Rohit – Credits AED 200; and Ram – Credits AED 500.

●✴︎✴︎✴︎✴︎✴︎✴︎✴︎✴︎❀✴︎✴︎✴︎✴︎✴︎✴︎✴︎✴︎✴︎●

           Hi my lil bunny!

❧⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯☙

                    [tex]\boxed{x = 7}[/tex]

Move 1 to the left side of the equation by subtracting it from both sides.

[tex]\sqrt{2x -5 - 2 - 1 = 0 }[/tex]

Subtract 1 from -2.

[tex]\sqrt{2x -5 - 3 = 0 }[/tex]

Add 3 to both sides of the equation.

[tex]\sqrt{2x - 5 = 3}[/tex]

To remove the radical on the left side of the equation, square both sides of the equation.

[tex]\sqrt{2x - 5^3 = 3^2}[/tex]

Simplify each side of the equation.

Multiply the exponents in [tex](( 2x - 5) ^\frac{1}{2})^2[/tex] .

Apply the power rule and multiply exponents, [tex](a^m)^n = a^mn[/tex]

[tex](2x -5)^\frac{1}{2}.2 = 3^2[/tex]

Cancel the common factor of 2.

[tex](2x - 5)^1 = 3^2[/tex]

Simplify.

[tex]2x - 5 = 3^2[/tex]

Raise 3 to the power of 2.

[tex]2x - 5 = 9[/tex]

Solve for x

Move all terms not containing x to the right side of the equation.

Add 5  to both sides of the equation.

[tex]2x = 9 + 5[/tex]

Add 9 and 5.

[tex]2x = 14[/tex]

Divide each term by 2  and simplify.

Divide each term in 2x = 14 by 2.

[tex]\frac{2x}{2} = \frac{14}{2}[/tex]

Cancel the common factor of 2.

[tex]x = \frac{14}{2}[/tex]

Divide 14 by 2.

[tex]x = 7[/tex]

❧⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯☙

●✴︎✴︎✴︎✴︎✴︎✴︎✴︎✴︎❀✴︎✴︎✴︎✴︎✴︎✴︎✴︎✴︎✴︎●

Hope this helped you.

Could you maybe give brainliest..?

❀*May*❀

Answer:

root of f(x) =  -0.7419124700395855 to about 16 figures

Step-by-step explanation:

given

f(x) = 2x^5-x^2+1 = 0

The polynomial is prime, so cannot solve by factoring.

Since it is a 5th degree polynomial, it has at least one real root.

Graphing helps locate where roots are, if more than one.

(refer to first graph)

So there is a real root between -1 and 0.

We will use numerical methods to find the root to a good degree of accuracy.  The technique applies to any univariable function which is differentiable and continuous near the roots.  This requirement is true for all polynomials.

However, we must know approximately where the root is, usually found by graphing.

The formula used is a recursive one, which gives a better approximation (x1) from the initial (x0) one , and can be repeated until the required accuracy is reached.

Here, we see that the slope of the function at the root is quite steep, so convergence will be rapid.

The formula is

x1 = x0 - f(x0) / f'(x0), where

x1 = new approximation

x0 = initial (or previous) approximation

f(x0) = value of function when x=x0

f'(x0) = value of derivative of function when x=x0

For the given function

f(x) = 2x^5-x^2+1 = 0

f'(x) = 10x^4-2x = 2x(5x^3-1)

From the graph of f(x), we can take an initial approximation as

x0 = -1

x1 = -1 - (-2)/12 = -5/6

Repeat using x0=-5/6

x1 = -5/6 - ( 2(-5/6)^5 - (-5/6)^2 + 1 ) / (2(-5/6(5(-5/6)^3-1))

= 0.7565596512088784

Repeat again, multiple times

x1 = -0.7423377914518363

x1 = -0.7419128371988212

x1 = -0.7419124700398593

x1 = -0.7419124700395855

x1 = -0.7419124700395855

So we see that the root of f(x) = x1 = -0.7419124700395855 to about 16 figures

Note that the accuracy of the iterations approximately doubles every time.

Answer:

3 years

Step-by-step explanation:

I assume it's simple interest.

I = Prt

132 = 800 * 0.055 * t

t = 132/(800 * 0.055)

t = 132/44

t = 3

Answer: 3 years

Answer:

A

Step-by-step explanation:

The blue graph, g(x), is shifted down 8 units.

So the answer is f(x)-8 which is A

Answer:  C. g(x) = eˣ⁻¹ - 3

Step-by-step explanation:

g(x) is a vertical shift 8 units down (-8) from f(x)

f(x) = eˣ⁻¹ + 5

g(x) = (eˣ⁻¹ + 5) - 8

      = eˣ⁻¹ - 3

Answer:

The five number summary are;

The minimum is 198

The 1st quartile, Q₁, is 205

The 2nd quartile, Q₂, or  median is 214

The 3rd quartile, Q₃, is 228

The Maximum is 237

Step-by-step explanation:

The numbers are;

232, 198, 214, 205, 222, 228, 208, 237, 217, 199, 213, 208, 228, 224, 203

Which can be rearranged in increasing order as follows;

198, 199, 203, 205, 208, 208, 213, 214, 217, 222, 224, 228, 228, 232, 237

The five number summary are;

The minimum = The lowest number in the list = 198

The 1st quartile, Q₁,  is the (n + 1)/4 th term which is (15 + 1)/4 = 4th term = 205

The 2nd quartile, Q₂, or  median is the (n + 1)/2 th term which is (15 + 1)/2 = 8th term = 214

The 3rd quartile, Q₃, is the 3×(n + 1)/4 th term which is 3×(15 + 1)/4 = 12th term = 228

The Maximum = The highest number in the list = 237.

Answer:

No

Step-by-step explanation:

0.99 is not a repeating decimal because it terminates, meaning that it "ends". We know this because there are no more digits after 9 and there is no "..." at the end of the decimal.

Answer:

The equation is true

Step-by-step explanation:

The best way to check if this equate is true is to convert the pi in radians to degree and actually evaluate the trigonometric terms.

Mathematically we know that pi = 180 degrees

So pi/8 = 22.5

and pi/4 = 180/4 = 45

So let’s make our check.

Insert pi = 22.5 and pi = 45

So we have;

tan 22/5 = √(1-cos45)/(1+cos45)

Now let’s evaluate this using a calculator.

tan 22/5 = 0.414213562373

The term in the root; 0.171572875254

The square root of this number is

0.41421356237

This is exactly as what is obtained with the tan 22.5

So we conclude that what we have is true

Answer:

1.63

HOPE THIS WILL HELP..............!

Answer:

Hey there!

You would use the HL theorem, because these are both right triangles, and have two lengths congruent to each other.

Hope this helps :)

Answer:

C. The interquartile range is 55

Step-by-step explanation:

When you want to find the interquartile range you look at the box plot to see that it is everything from the upper interquartile range to the lower interquartile range is the interquartile range. So from 40 to 65. So there for the answer C. is incorrect.  

Answer:

A.

Step-by-step explanation:

Answer:

[tex]h=30[/tex]

Step-by-step explanation:

Volume of a cone=1540[tex]cm^{3}[/tex], Radius=7cm.

The height of a cone=h

When we need to find the height of a cone, we can use the formula of the volume of a cone, which is [tex]\frac{1}{3} \pi r^{2} h[/tex] to find the height of a cone.

[tex]1540cm^{3} =\frac{1}{3}\pi r^{2} h[/tex]

Put the pi value=22/7 and the value of radius which is 7 cm into the formula.

[tex]1540cm^{3}=\frac{1}{3}*\frac{22}{7} 7^{2}h[/tex]

[tex]1540cm^{3} =\frac{154}{3}h[/tex]

Move [tex]\frac{154}{3}[/tex] to another side. 1540 divided by  [tex]\frac{154}{3}[/tex] to calculate what is the value of h, h is the height of a cone. Like this.

[tex]\frac{1540cm^{3} }{\frac{154}{3} } =h[/tex]

[tex]30=h[/tex]

Rearrange the h.

[tex]h=30[/tex]

I hope you will understand my solution and explanation. If you still cannot get the point, you can ask me anytime! Thank you!

Answer:

The height of the cone is h = 30 cm.

Step-by-step explanation:

The formula for a cone is:

[tex] \\ V = \frac{1}{3}*\pi*r^2*h[/tex]

We have (without using units) and using pi = 22/7:

[tex] \\ 1540 = \frac{1}{3}*\frac{22}{7}*(7)^2*h[/tex]

Which is equals to:

[tex] \\ 1540 = \frac{1}{3}*\frac{22}{7}*(7)*h[/tex]

[tex] \\ 1540 = \frac{1}{3}*22*7*h[/tex]

Well, we have to solve the equation for h:

[tex] \\ \frac{1540*3}{22*7} = h[/tex]

[tex] \\ 30 = h[/tex]

Therefore, the height of the cone is 30 cm.

Answer:900

Step-by-step explanation:

Answer:

960 cm.

Step-by-step explanation:

For the first day:

Subtract the primary level of water by the 20% of it. 20% of 1500 is:

[tex]0.2*1500=300[/tex] (Convert the percent to decimal)

Then subtract 1500 to 300. That would become 1200cm for the first day.

For the second day:

Subtract the level of water from the first day by 20% of it. 20% of 1200 is:

[tex]0.2*1200= 240[/tex]

Then subtract 1200 to 240. That would become 960 for the second day.

The level of the water after 2 days is 960 cm.

Answer:

2x²+5x+2=(2x+1)(x+2)

Answer:

See details below

Step-by-step explanation:

in ax^2+bx+c = 2x^2+5x+2,

a=2,b=5,c=2.

1. a*c = 2*2 = 4

2. factor 4 to get 1,2,4,  Factors that add to b=5 are 1 & 4.

3. (2x^2+x) + (4x+2)

4. x(2x+1) + 2(2x+1)

5. (2x+1)

6. (2x+1) ( x+2)

Some of the details may not be the same as what is expected as we do not know the format expected.

Answer:

67 degrees

Step-by-step explanation:

alternate exterior angles are always congruent

Answer:

The value of y is 67°.

Step-by-step explanation:

Here, given that;

BD is parallel to XY. let EF be a transversal line meeting BD at O and XY at P.

now, angle XQF = 67°

now, angle XQF + angle YQF=180° (being linear pair)

or, 67°+angle YQF =180°

or, angle YQF=180°-67°

therefore angle YQF = 113°.

now, angle YQF + angle PQY=180° (being linear pair).

now, 113°+angle PQY = 180°.

or, angle PQY = 180°-113°.

therefore, angle PQY =67°.

again, angle EPD= angle PQY (being corresponding angles).

or, y°= 67°.

Therefore the value of y is 67°.

hope it helps...

Answer:

The shortest path to take is [tex]20\sqrt{3}\ cm[/tex] or [tex]34.64\ cm[/tex]

Step-by-step explanation:

This question requires an attachment (See attachment 1 for question)

Given

Cube Dimension: 20cm * 20cm

Required

Shortest path from A to B

For proper explanation, I'll support my answer with an additional attachment (See attachment 2)

The shortest path from A to B is Line labeled 2

But first, the length of line labeled 1 has to be calculated;

This is done as follows;

Since, the cube is 20 cm by 20 cm

[tex]Line1^2 = 20^2 + 20^2[/tex] (Pythagoras Theorem)

[tex]Line1^2 = 2(20^2)[/tex]

Take square root of both sides

[tex]Line1 = \sqrt{2(20)^2}[/tex]

Split square root

[tex]Line1 = \sqrt{2} * \sqrt{20^2}[/tex]

[tex]Line1 = \sqrt{2} * 20[/tex]

[tex]Line1 = 20\sqrt{20}[/tex]

Next is to calculate the length of Line labeled 2

[tex]Line2^2 = Line1^2 + 20^2[/tex] (Pythagoras Theorem)

Substitute [tex]Line1 = 20\sqrt{20}[/tex]

[tex]Line2^2 = (20\sqrt{2})^2 + 20^2[/tex]

Expand the expression

[tex]Line2^2 = (20\sqrt{2})*(20\sqrt{2}) + 20 * 20[/tex]

[tex]Line2^2 = 400*2 + 400[/tex]

Factorize

[tex]Line2^2 = 400(2+1)[/tex]

[tex]Line2^2 = 400(3)[/tex]

Take square root of both sides

[tex]Line2 = \sqrt{400(3)}[/tex]

Split square root

[tex]Line2 = \sqrt{400} * \sqrt{3}[/tex]

[tex]Line2 = 20 * \sqrt{3}[/tex]

[tex]Line2 = 20 \sqrt{3}[/tex]

The answer can be left in this form of solve further as follows;

[tex]Line2 = 20 * 1.73205080757[/tex]

[tex]Line2 = 34.6410161514[/tex]

[tex]Line2 = 34.64 cm[/tex] (Approximated)

Hence, the shortest path to take is [tex]20\sqrt{3}\ cm[/tex] or [tex]34.64\ cm[/tex]

Answer:

44.72 cm

Step-by-step explanation:

1. This was marked correct by RSM

2. Unfold the cube, so that points A and B and on points diagonal from each other on a 40 cm x 20 cm rectangle. Now draw a line connecting points A to B. That is the hypotenuse of both triangles. Now according to the pythagorean theorem, the hypotenuse is √2000, which is equal to 5√20.

3. The answer is 44.72 cm

Answer:

[tex]\boxed{\±\sqrt{x+4}}[/tex]

Step-by-step explanation:

The inverse of a function is the reverse of the function.

[tex]f(x)=x^2 -4[/tex]

[tex]y=x^2-4[/tex]

Switch variables.

[tex]x=y^2-4[/tex]

Make y as subject.

Add 4 to both sides.

[tex]x+4=y^2[/tex]

Take the square root on both sides.

[tex]\±\sqrt{x+4} =y[/tex]

Answer:

[tex]f^{-1}[/tex] = ± [tex]\sqrt{x+4}[/tex]

Step-by-step explanation:

[tex]f(x) = x^2-4[/tex]

Replace f(x) by y

[tex]y = x^2-4[/tex]

Exchange x and y

[tex]x = y^2-4[/tex]

Solve for y

[tex]x = y^2-4\\[/tex]

Adding 4 to both sides

[tex]y ^2 = x+4[/tex]

Taking sqrt on both sides

y = ±[tex]\sqrt{x+4}[/tex]

Replacing y by [tex]f^{-1}[/tex]

[tex]f^{-1}[/tex] = ± [tex]\sqrt{x+4}[/tex]

Answer:

From Plato

30e-0.12t less than or equal to M

40e-0.18t less than or equal to M

Step-by-step explanation:

It is given that compound A decays at a rate of 12% per week, and compound B decays at a rate of 18% per week. Since the rates represent decay, the r-value is negative. A decay rate of 12% is represented by an r-value of -0.12, and a decay rate of 18% is represented by an r-value of -0.18.

The initial amount of compound A is 30 grams and the initial amount of compound B is 40 grams. Substitute the initial amounts of each compound and their respective decay rates into the system of inequalities.

The following system of inequalities can be used to determine when the remaining mass of the two compounds, M, will be the same, after t weeks.