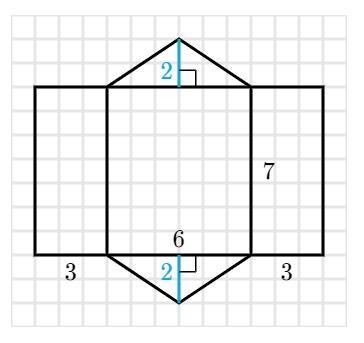
Answers
Answer:
It is 96 square units
Step-by-step explanation:
Related Questions
In a simple regression analysis for a given data set, if the null hypothesis β = 0 is rejected, then the null hypothesis ρ = 0 is also rejected. This statement is ___________ true. always
Answers
Answer:
Null hypothesis: [tex]\rho =0[/tex]
Alternative hypothesis: [tex]\rho \neq 0[/tex]
The statistic to check the hypothesis is given by:
[tex]t=\frac{r \sqrt{n-2}}{\sqrt{1-r^2}}[/tex]
And is distributed with n-2 degrees of freedom
And the statistic to check the significance of a coeffcient in a regression is given by:
[tex] t_1 = \frac{\hat{\beta_1} -0}{S.E (\hat{\beta_1})}[/tex]
For this case is importantto remember that t1 and p value for test of slope coefficient is the same test statistic and p value for the correlation test so then the answer would be:
Always
Step-by-step explanation:
In order to test the hypothesis if the correlation coefficient it's significant we have the following hypothesis:
Null hypothesis: [tex]\rho =0[/tex]
Alternative hypothesis: [tex]\rho \neq 0[/tex]
The statistic to check the hypothesis is given by:
[tex]t=\frac{r \sqrt{n-2}}{\sqrt{1-r^2}}[/tex]
And is distributed with n-2 degrees of freedom
And the statistic to check the significance of a coeffcient in a regression is given by:
[tex] t_1 = \frac{\hat{\beta_1} -0}{S.E (\hat{\beta_1})}[/tex]
For this case is importantto remember that t1 and p value for test of slope coefficient is the same test statistic and p value for the correlation test so then the answer would be:
Always
find the maximal area of a right triangle with hypotenuse of length 8
Answers
Answer:
Max area is 16
Step-by-step explanation:
If A² + B² = C², then A² + B² = 64. The largest triangle area is when both A² and B² are equal to 32, so 32 + 32 = 64.
So equal side of the triangle is √32 or about 5.6568. The area of the triangle is then 1/2(5.6568 × 5.6568) or 16.
The maximal area of a right triangle is 90.496
What is differentiation?Derivative of a function of a real variable measures the sensitivity to change of the function value with respect to a change in its argument. Derivatives are a fundamental tool of calculus.
Given:
let the perpendicular be 'x'
and base be 'y'
Using Pythagoras theorem
x² + y² = 8²
x² + y² = 64
y²= 64- x²
y = √64-x²
Now, Area of triangle
= 1/2* base* height
=xy/2
=x *√64-x²*1/2
On differentiating both side
A' = 64-2x²/√64-x²*1/2
Setting derivative function equal to zero,
64= 2x²
32=x²
x=5.656
So, Area of triangle = x *√64-x²*1/2
= 90.496
Learn more about differentiation here:
https://brainly.com/question/24898810
#SPJ2
by what number 7whole 2/3be divided to get 4whole1/3
Answers
Answer: 1 30/39
Step-by-step explanation:
Because y/x=z and y/z=x are true with the same values, simply do 7 2/3 divided by 4 1/3 to get 69/39.
Hope it helps <3
please please
please
please help
me. i am desperate
Answers
Answer:The answer is c
Step-by-step explanation:
Find the probability of picking 1 consonant and 4 vowels when 5 letters are picked (without replacement) from a set of alphabet tiles.
Answers
Answer:
Ok, we have a total of 26 letters, and we want to select 5 of them.
Of the 26 letters, 21 are consonants and 5 are vowels.
Suppose that we want to have the consonant in the first selection, so the probability of picking a consonant is equal to the quotient between the number of consonants and the total number of letters.
p = 21/26
now a letter has been selected, so in the set, we have 25 letters left.
In the next 4 selections, we must select vowels.
In the second selection the probability is:
p = 5/25
in the third, the prob is:
p = 4/24 (we already selected one vowel before, so now we only have 4 vowels)
The fourth selection:
p = 3/23
and the last selection:
p = 2/22
The total probability is equal to the product of all the individual proabilities, so we have:
P = (2/22)*(3/23)*(4/24)*(5/25)*(21/26)
Now, remember that we said that the consonant must be in the first place, but it can be in any of the five places, so if we add the permutations of the consonant letter we have:
P = 5*(2/22)*(3/23)*(4/24)*(5/25)*(21/26) = 0.0018
Witch table represents a linear function ?
Answers
Answer:
If you compute the slope between any two points that must be the same, that's how you can tell if a table represents a linear function.
Remember that the slope between any two points (x1,y1), (x2,y2) is
slope = ( y2 - y1 ) / (x2 - x1)
Step-by-step explanation:
If you compute the slope between any two points that must be the same, that's how you can tell if a table represents a linear function.
Remember that the slope between any two points (x1,y1), (x2,y2) is
slope = ( y2 - y1 ) / (x2 - x1)
Dunno these answers
Answers
Answer:
its 9
Step-by-step explanation:
Answer:
c. 9i.
Step-by-step explanation:
[tex]\sqrt{-81}[/tex]
= [tex]\sqrt{-1 * 9 * 9}[/tex]
= [tex]\sqrt{-1 * 9^2}[/tex]
= [tex]9\sqrt{-1}[/tex]
The square root of -1 is the same thing as i.
= [tex]9i[/tex]
So, your answer is C.
Hope this helps!
what is the slop of y= -5+4x
Answers
Hey there! :)
Answer:
m = 4.
Step-by-step explanation:
We are given the formula y = -5 + 4x. Rearrange the equation to be in proper slope-intercept form (y = mx + b)
Where 'm' is the slope and 'b' is the y-intercept. Therefore:
y = -5 + 4x becomes y = 4x - 5
The 'm' value is equivalent to 4, so the slope of the equation is 4.
Answer:
4
Step-by-step explanation:
because of y= mx + b where m is the slope
m= 4 in the equation
how many two third ounce slice of cheese in twenty four ounce package
Answers
Answer: 36
Step-by-step explanation:
Simply do 24/(2/3) to get 36 2/3 ounce slices.
Hope it helps <3
Which best describes the meaning of the statement if A then B
Answers
Answer:
[tex]a => b \equiv ( \neg a \ \lor \ b )[/tex]
Step-by-step explanation:
You can understand the statement from many perspectives, but in terms of proposition logic it is best to understand it as "negation of a" or " b" in mathematical terms is written like this
[tex]a => b \equiv ( \neg a \ \lor \ b )[/tex]
You can show that they are logically equivalent because they have the same truth table.
Total score: ____ of 20 points A marching band performs on the football field at half-time. As they perform, the members of the band stand in the shape of a sinusoidal function. While playing, they move, but still maintain the sinusoidal function, transforming it in different ways. Darla is a member of the marching band. As the band begins to play she is positioned in the exact center of the field. The person closest to her on the same horizontal line, stands 10 yards away. The sinusoidal function extends to the ends of the playing field. The playing area of football field measure 300 feet by 160 feet. Place the playing area of a football field on the coordinate plane such that the origin is the lower left corner of the football field. (Score for Question 1: ___ of 2 points) 1. What is the period and the amplitude of the sine function representing the position of the band members as they begin to play? Answer: (Score for Question 2: ___ of 6 points) 2. Edna is sitting in the stands and is facing Darla. Edna observes that sine curve begins by increasing at the far left of the field. What is the equation of the sine function representing the position of band members as they begin to play? Answer: (Score for Question 3: ___ of 4 points) 3. As the band begins to play, band members move away from the edges, and the curve reverses so that the function begins at the far left by decreasing. Darla does not move. The sine curve is now half as tall as it was originally. What is the equation of the sine curve representing the position of the band members after these changes? Answer: (Score for Question 4: ___ of 3 points) 4. Next, the entire band moves closer to the edge of the football field so that the sine curve is in the lower half of the football field from Edna’s vantage point. What is the equation of the sine curve representing the position of the band members after these changes? Answer: (Score for Question 5: ___ of 5 points) 5. At the end of the performance, the band marches off the field to the right, moving the entire sine curve. Asa grabs his camera to takes a picture of the entire football field. At the instant he takes the picture, the first person forming the curve now stands at the 5 yard line. What is the equation of the sine curve representing the position of the band members in Asa’s picture? Answer: Please help me explain step-by-step thank you
Answers
Answer:
1) Amplitude; A = 80 ft
Period = 60 ft
2)y = 80 sin ((π/30)x - 5π) + 80
3)y = 40 sin ((π/30)x - 5π) + 80
4)y = 40 sin ((π/30)x - 5π) + 40
5)y = -65sin ((π/30)x - 5π) + 80
Step-by-step explanation:
The general formula for sinusoidal wave equation is given by;
y = A sin (Bx - C) + D
Where;
A is amplitude = D_max or D_min
Period = 2π/B
So; B = 2π/Period
Phase Shift = C/B
So; C = B · Phase Shift
D: center
We are Given:
Height of the field is 160 ft and so the center is at y = 80. Thus; D = 80 ft
Thus; A = 80 ft
The person closest to Darla on the same horizontal line, stands 10 yards(30 ft) Thus, period = 2 × 30 = 60 ft
Thus; B = 2π/60 = π/30
Field is 300 ft wide and so the center is 300/2 = 150 ft
Thus; Phase Shift = 150.
C = B × Phase Shift = π/30 · 150 = 5π
1) From the calculations above,
Amplitude; A = 80 ft
Period = 60 ft
2) As they begin to play, from the calculations above and y = A sin (Bx - C) + D, equation of the sine function is now;
y = 80 sin ((π/30)x - 5π) + 80
3) In this, since the sine wave is half as tall, then after the changes, we have;
y = 40 sin ((π/30)x - 5π) + 80
4) since they have moved closer, then equation is now;
y = 40 sin ((π/30)x - 5π) + 40
5) We are Given:
Height of the field is 160 ft and so the center is at y = 80. Thus; D = 80 ft
Since the first person forming the curve now stands at the 5 yard line, the minimum is at 5 yds (15 ft). Thus;
D_min = 80 - 15 = 65. Thus; A = 65 ft
The person closest to Darla on the same horizontal line, stands 10 yards(30 ft) Thus, period = 2 × 30 = 60 ft
Thus; B = 2π/60 = π/30
Field is 300 ft wide and so the center is 300/2 = 150 ft
Thus; Phase Shift = 150.
C = B × Phase Shift = π/30 · 150 = 5π
The band ends down (at 15 feet) and thus A is negative
The equation is;
y = -65sin ((π/30)x - 5π) + 80
Part(1): The required values are,
Amplitude=[tex]80 ft[/tex] and Period: [tex]60 sec[/tex]
Part(2):
The equation of the sine function is
[tex]y=80 cos(\frac{\pi x}{30}+\pi)+80[/tex]
Part(3):
The equation of the sine curve is,
[tex]y=40cos(\frac{\pi x}{30})+80[/tex]
Part(4):
The equation of the sine curve representing the position of the band members after these changes is [tex]y=40cos(\frac{\pi x}{30})+40[/tex]
Part(5):
The required graph is attached below,
Simple harmonic motion:Simple Harmonic Motion or SHM is defined as a motion in which the restoring force is directly proportional to the displacement of the body from its mean position
Part(1):
Amplitude=[tex]\frac{1}{2} width=80ft[/tex]
Period=[tex]2\times 30=60 sec[/tex]
Part(2):
Let the equation be,
[tex]y=80 cos(\frac{\pi x}{30}+\pi)+80\\ y'=-\frac{8\pi}{3} sin((\frac{\pi x}{30}+\pi))[/tex]
Darla is at the point [tex]D(150,80)[/tex] which is on the graph at [tex]x=0[/tex] then,
[tex]80=80 cos(5\pi+\pi)=0\\y=-80 cos (\frac{\pi x}{30} )+80[/tex]
Part(3):
Since the wave is now [tex]\frac{160}{2} =80 ft[/tex] then,
Amplitude=40 ft
[tex]y=-4 cos (\frac{\pi x}{30} -\pi)+80\\y=40cos(\frac{\pi x}{30})+80[/tex]
Part(4):
The graph shifts downward 40 ft then,
[tex]y=-4 cos (\frac{\pi x}{30} -\pi)+80-40\\y=40cos(\frac{\pi x}{30})+40[/tex]
Part(5):
Start at:[tex]Y(x)=80sin (\frac{2\pi x}{60} )+80\\[/tex]
End at: [tex]Z(x)=80sin[ (\frac{2\pi }{60}(x-15) )]+80\\[/tex]
The graph is attached below:
Learn more about the topic of Simple harmonic motion:
https://brainly.com/question/14446439
Please answer in the form of a number
Answers
Answer:
d ≈ 8.3
Step-by-step explanation:
This is kind of like the pythagorean theorem, but with one extra value. Thus, [tex]d^2=l^2+w^2+h^2[/tex].
Plug in the values to get:
[tex]d^2=2^2+7^2+4^2\\d^2=4+49+16\\d^2=69\\d=\sqrt{69} \\[/tex]
Thus d ≈ 8.3
The slope intercept form of a line is
y=mx+b
The slope is represented by____
The y-intercept is represented by____
Answers
Answer:y=Mx+b
Step-by-step explanation:
Solve for y in terms of x.
IN
2
y - 4 = x
Oy= = x + 6
Oy
y = -x + 4
Oy
y = -x + 6
O
y =
X+ 4
Answers
Answer:
[tex]\boxed{\mathrm{Option \ 4}}[/tex]
Step-by-step explanation:
Given that
[tex]y-4 = x[/tex]
Adding 4 to both sides
[tex]y-4+4 = x+4\\[/tex]
[tex]y = x+4[/tex]
PLEASE HELP ME UNDERSTAND!! ok, when i looked at other people converting sin, cos, tan, i realized this; cos(x) = y/z z = y cos(x) which is weird. why would you multiply cos by y instead of dividing cos by y?
Answers
Answer:
the real deal is that you mistook if
cos(x)=y/z gives y=zcos(x)
If four times the brother's age is subtracted from three times the sister's age, the difference is 17. Give an equation that represents this statement using bbb as the age of the brother and s as the age of the sister.
Answers
Answer:
3s-4bbb=17
Step-by-step explanation:
brother=4bbb
sister=3s
3s-4bbb=17
PLEASE HELP
Divide. Write your answer using the smallest numbers possible. 47 pounds 13 ounces divided by 15 = ___pounds ___ounces
Answers
Answer:
3 pounds
51 ounces
Step-by-step explanation:
James determined that these two expressions were equivalent expressions using the values of x - 4 and x-6.
Which statements are true? Check all that apply.
7x+4 and 3x+5+4x-1
When x-2, both expressions have a value of 18.
The expressions are only equivalent for x = 4 and x-6.
The expressions are only equivalent when evaluated with even values.
The expressions have equivalent values for any value of x.
The expressions should have been evaluated with one odd value and one even value.
When x-0, the first expression has a value of 4 and the second expression has a value of 5.
The expressions have equivalent values if x - 8.
Answers
Answer:
1 - Correct
2 - incorrect
3- incorrect
4 - incorrect
5 - Correct
Step-by-step explanation:
Notice that
3x + 5 + 4x -1 = 3x + 4x + 5 -1 = 7x + 4
therefore the two expressions are equivalent for ANY number, specially x = 4 and x = 6 therefore
1 - Correct
Since that is true for all numbers
2 - incorrect
3- incorrect
4 - incorrect
The expressions are equivalent for all numbers therefore
5 - Correct
4.5/y = 12.5/4 PLEASE HELP!!! SOS
Answers
Answer:
y = 1.44
Step-by-step explanation:
What are you aiming to do here? Please share all instructions with each problem.
If you want to solve 4.5/y = 12.5/4 for y: Multiply both sides by 4y:
18 = 12.5y. Then y = 1.44
The height of a projectile launched upward at a speed of 32 feet/second from a height of 128 feet is given by the function h(t) = -16t^2 + 32t +128. How long will it take the projectile to hit the ground?
Answers
Answer:
It takes 4 seconds for the projectile to hit the ground
Step-by-step explanation:
The height of the projectile after t seconds is given by the following equation:
[tex]h(t) = -16t^{2} + 32t + 128[/tex]
How long will it take the projectile to hit the ground?
It happens when [tex]h(t) = 0[/tex]
So
[tex]h(t) = -16t^{2} + 32t + 128[/tex]
[tex]-16t^{2} + 32t + 128 = 0[/tex]
Solving a quadratic equation:
Given a second order polynomial expressed by the following equation:
[tex]ax^{2} + bx + c, a\neq0[/tex].
This polynomial has roots [tex]x_{1}, x_{2}[/tex] such that [tex]ax^{2} + bx + c = a(x - x_{1})*(x - x_{2})[/tex], given by the following formulas:
[tex]x_{1} = \frac{-b + \sqrt{\bigtriangleup}}{2*a}[/tex]
[tex]x_{2} = \frac{-b - \sqrt{\bigtriangleup}}{2*a}[/tex]
[tex]\bigtriangleup = b^{2} - 4ac[/tex]
In this question:
[tex]-16t^{2} + 32t + 128 = 0[/tex]
So [tex]a = -16, b = 32, c = 128[/tex]
[tex]\bigtriangleup = 32^{2} - 4*(-16)*(128) = 9216[/tex]
[tex]t_{1} = \frac{-32 + \sqrt{9216}}{2*(-16)} = -2[/tex]
[tex]t_{2} = \frac{-32 - \sqrt{9216}}{2*(-16)} = 4[/tex]
Time is a positive measure, so:
It takes 4 seconds for the projectile to hit the ground
What is the equation of the line perpendicular to y=5x-3 that passes through the point (3, 5)?
Answers
Answer:
[tex]y=-\frac{1}{5}x\ +\ 5.6[/tex]
Step-by-step explanation:
Hey there!
Well the slope of the perpendicular line is -1/5 because that's the reciprocal of 5.
Look at the image below ↓
By looking at the image we can conclude that the equation for the perpendicular line is,
[tex]y=-\frac{1}{5}x\ +\ 5.6[/tex].
Hope this helps :)
Answer:
[tex]\boxed{y=-\frac{1}{5}x+\frac{28}{5}}[/tex]
Step-by-step explanation:
Part 1: Finding the new slope of the line
Perpendicular lines have reciprocal slopes of a given line - this means that the slope you are given in the first equation will be flipped and negated.
Because the slope is 5 in the first line, it gets flipped to become [tex]-\frac{1}{5}[/tex].
Part 2: Using point-slope formula and solving in slope-intercept form
Input the new slope into the slope-intercept equation: [tex]y=mx+b[/tex]. This results in [tex]y=-\frac{1}{5} x+b[/tex].
Then, use the point-slope equation to get b, or the y-intercept of the equation.
[tex](y-y_{1})=m(x-x_{1})[/tex]
[tex](y-5)=-\frac{1}{5}(x-3)\\\\y-5=-\frac{1}{5}x+\frac{3}{5} \\\\y=-\frac{1}{5}x+\frac{28}{5}[/tex]
An ice sculpture is melting at a constant rate. It's weight changes -1 4/5 pounds every hour. What is the total change in weight of the sculpture after 3 1/2 hours?
Answers
Answer:
It will decrease by 6 3/10 lbs in the 3 1/2 hours
Step-by-step explanation:
The rate is -1 4/5 lbs per hour
The time is 3 1/2 hours
Multiply to find the weight change
-1 4/5 * 3 1/2
Change to improper fractions
- ( 5*1 +4) /5 * ( 2* 3+1)/2
- 9/5 * 7/2
-63/10
Changing back to a mixed number
-6 3/10
It will decrease by 6 3/10 lbs in the 3 1/2 hours
Answer:
-6 3/10 pounds
Step-by-step explanation:
The weight of ice sculpture changes -1 4/5 pounds every 1 hour.
In 3 1/2 hours, multiply the time with the weight.
-1 4/5 × 3 1/2
Multiply.
-9/5 × 7/2
-63/10 = -6 3/10
if -2x = -14 what is the value of x
Answers
Answer: x= 7
Step-by-step explanation:
-2x= -14 Divide both sides by -2
x= 7
check
-2(7) = -14
-14 = -14
Answer:
x = 7
Step-by-step explanation:
-2x = -14
Divide each side by -2
-2x/-2 = -14/-2
x = 7
Two passenger trains traveling in opposite directions meet and pass each other. Each train is 1 12 mi long and is traveling 50 mph. How many seconds after the front cars of the trains meet will their rear cars pass each other?
Answers
Answer:
Time taken = 6 sec (Approx)
Step-by-step explanation:
Given:
Total distance = 1/12 mi = 0.083333
Speed of train = 50 mph = 50 / 3600 = 0.01388889 mps
Find:
Time taken
Computation:
Time taken = Total distance / Speed
Time taken = Total distance / Speed of train
Time taken = 0.0833333 / 0.01388889
Time taken = 6 sec (Approx)
What is the correct slope and y-intercept for the following: y=-3x+8
Answers
━━━━━━━☆☆━━━━━━━
▹ Answer
Slope = -3
Y-intercept = 8
▹ Step-by-Step Explanation
y = mx + b
mx represents the slope.
b represents the y intercept.
therefore,
y = -3x + 8
Hope this helps!
CloutAnswers ❁
Brainliest is greatly appreciated!
━━━━━━━☆☆━━━━━━━
Answer:
[tex]\boxed{\mathrm{Slope:}-3 \: \: \: \:\: \mathrm{Y \: intercept:}8}[/tex]
Step-by-step explanation:
The general form of slope-intercept:
[tex]y=mx+b[/tex]
[tex]m:slope\\b:y \: intercept[/tex]
[tex]y=-3x+8[/tex]
[tex]m=-3\\b=8[/tex]
The slope is -3.
The y-intercept is (0, 8) or 8.
Use implicit differentiation to find an equation of the tangent line to the curve at the given point.
x2 + y2 = (4x2 + 2y2 − x)2
(0, 0.5)
(cardioid)
Answers
Answer:
y = x + 0.5
Step-by-step explanation:
This is a very trivial exercise, follow the steps below:
Step 1: Perform the implicit differentiation of the given equation
[tex]x^2 + y^2 = (4x^2 + 2y^2 - x)^2[/tex]
[tex]2x + 2y \frac{dy}{dx} = 2(4x^2 + 2y^2 - x) ( 8x + 4y\frac{dy}{dx} - 1)\\\\[/tex]
Step 2: Make dy/dx the subject of the formula, this will be the slope of the curve:
[tex]x + y \frac{dy}{dx} = (4x^2 + 2y^2 - x) ( 8x + 4y\frac{dy}{dx} - 1)\\\\x + y \frac{dy}{dx} = 32x^3 + 16x^2y \frac{dy}{dx} - 4x^2 + 16xy^2 + 8y^3\frac{dy}{dx} - 2y^2 - 8x^2 - 4xy\frac{dy}{dx} + x \\\\\frac{dy}{dx}(y + 4xy - 8y^3) = 32x^3 - 12x^2 + 16xy^2 - 2y^2\\\\\frac{dy}{dx} = \frac{32x^3 - 12x^2 + 16xy^2 - 2y^2}{y + 4xy - 8y^3}[/tex]
Step 3: Find dy/dx at the point (0, 0.5)
[tex]\frac{dy}{dx}|(0,0.5) = \frac{32(0)^3 - 12(0)^2 + 16(0)(0.5)^2 - 2(0.5)^2}{(0.5) + 4(0)(0.5) - 8(0.5)^3}\\\\\frac{dy}{dx}|(0,0.5) =\frac{-0.5}{-0.5} \\\\\frac{dy}{dx}|(0,0.5) =1\\\\m = \frac{dy}{dx}|(0,0.5) =1[/tex]
Step 4: The equation of the tangent line to a curve at a given point is given by the equation:
[tex]y - y_1 = m(x-x_1)\\\\y - 0.5 = 1(x - 0)\\\\y = x + 0.5[/tex]
The volume of a rectangular prism is (x4 + 4x3 + 3x2 + 8x + 4), and the area of its base is (x3 + 3x2 + 8). If the volume of a rectangular prism is the product of its base area and height, what is the height of the prism?
Answers
Answer:
[tex]Height = x \frac{x^3+3x^2+4}{x^3+3x^2+8}[/tex]
Step-by-step explanation:
[tex]Volume = Base \ Area\ * Height[/tex]
[tex]Height = \frac{Volume}{Base \ Area}[/tex]
Where [tex]Volume = x^4+4x^3+8x+4[/tex] and [tex]Area = x^3+3x^2+8[/tex]
Putting in the formula
[tex]Height = \frac{x^4 + 4x^3 + 3x^2 + 8x + 4}{x^3 + 3x^2 + 8}[/tex]
Doing long division, we get
[tex]Height = x + \frac{x^3+3x^2+4}{x^3+3x^2+8}[/tex]
[tex]Height = x \frac{x^3+3x^2+4}{x^3+3x^2+8}[/tex]
This is the simplifies form and it can't be further simplified.
Answer:
[tex]x +1 - \frac{4}{x^3 + 3x^2 + 8}[/tex]
Step-by-step explanation:
[tex]volume=base \: area \times height[/tex]
[tex]height=\frac{volume}{base \: area}[/tex]
[tex]\mathrm{Solve \: by \: long \: division.}[/tex]
[tex]h=\frac{(x^4 + 4x^3 + 3x^2 + 8x + 4)}{(x^3 + 3x^2 + 8)}[/tex]
[tex]h=x + \frac{x^3 + 3x^2 + 4}{x^3 + 3x^2 + 8}[/tex]
[tex]h=x +1 - \frac{4}{x^3 + 3x^2 + 8}[/tex]
Find the 10th term of the following geometric sequence.
2, 10, 50, 250, ...
Answers
Answer:
3906250
Step-by-step explanation:
We can notice that the ratio is 5. 10/2 = 5
Each term gets multiplied by 5 to get the next term.
250 × 5 = 1250 (5th term)
1250 × 5 = 6250 (6th term)
6250 × 5 = 31250 (7th term)
31250 × 5 = 156250 (8th term)
156250 × 5 = 781250 (9th term)
781250 × 5 = 3906250 (10th term)
The 10th term of the geometric sequence is 3906250.
Which equation shows y-5=x converted to slope intercept form.
Answers
Answer:
C) y = x + 5
Step-by-step explanation
Add 5 to both sides
4, 12, 36,what is 3 other remaining sequence
Answers
Answer:
108, 324, 972
Step-by-step explanation:
This sequence is multiplying by ✖️3.
4✖️3=12✖️3=36✖️3=108✖️3=324✖️3=972
Hope this helps!