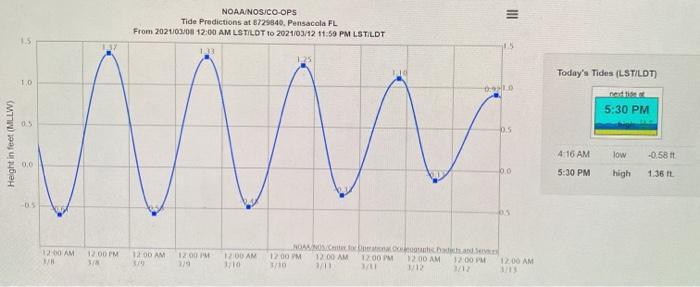
combined with a high tide on september 16, 2020 by how many feet did that storm surge submerge the lowest parts of pensacola beach? enter a number (no words) in the blank.

we can expect that approximately 815 employees owned a petrol car in 2019 (rounded to the nearest integer).

We can model the number of employees owning petrol cars in the years 2010 and 2013 using the exponential decay formula:

[tex]$$N(t) = N_0 e^{-kt}$$[/tex]

where N(t) is the number of employees owning petrol cars at time t, [tex]$N_0$[/tex] is the initial number of employees owning petrol cars (in 2010), k is the decay constant, and t is the time elapsed since 2010 (in years).

We can use the given information to find the value of k:

In 2013 (3 years after 2010), the number of employees owning petrol cars decreased from 2187 to 1536:

[tex]$$1536 = 2187 e^{-3k}$$[/tex]

Dividing both sides by 2187 gives:

[tex]$$e^{-3k} = \frac{1536}{2187}$$[/tex]

Taking the natural logarithm of both sides gives:

[tex]$$-3k = \ln\left(\frac{1536}{2187}\right)$$[/tex]

Solving for k gives:

[tex]$k = -\frac{1}{3} \ln\left(\frac{1536}{2187}\right) \approx 0.1565$$[/tex]

Now we can use the exponential decay formula to find the number of employees owning petrol cars in 2019 (9 years after 2010):

[tex]$$N(9) = 2187 e^{-0.1565 \cdot 9} \approx 815$$[/tex]

Therefore, we can expect that approximately 815 employees owned a petrol car in 2019 (rounded to the nearest integer).

To know more about Exponential function visit:

brainly.com/question/14355665

#SPJ1

a) r = 30 cm

b) The angle AOC is 0.523598775 radian

c) The area of the shaded region is 541.9 cm²

d) The perimeter of the shaded region is 106.8 cm.

The area of a circle is a measure of the size of the surface of the circle. It is calculated by multiplying the radius of the circle (the length from the center of the circle to its edge) by itself, and then multiplying the result by the constant pi (3.14). The formula for calculating the area of a circle is A = πr2, where “A” represents the area, “π” is pi, and “r” is the radius of the circle.

The radius of the circle, r, can be determined by the Pythagorean theorem. Since AC = 36 cm and AP = 6 cm, the hypotenuse of the right triangle formed by AC and AP is the radius of the circle, r. By applying the Pythagorean theorem, we get:

r² = 362 + 62

r² = 1296

r = √1296

r = 36 cm

b) The angle AOC is 0.523598775 radians

The angle AOC can be determined using the formula for arc length. The arc length of ABC is 36 cm and the radius of the circle is 30 cm. Therefore, the angle AOC is:

AOC = 36/30

AOC = 1.2 radians

c) The area of the shaded region is 541.9 cm²

The area of the shaded region can be determined using the formula for the area of a sector. The angle AOC is 1.2 radians and the radius of the circle is 30 cm. Therefore, the area of the shaded region is:

Area = (1.2)(30)(30)/2

Area = 541.9 cm²

d) The perimeter of the shaded region is 106.8 cm

The perimeter of the shaded region can be determined using the formula for the circumference of a circle. The radius of the circle is 30 cm. Therefore, the perimeter of the shaded region is:

Perimeter = 2π(30)

Perimeter = 106.8 cm

For more questions related to perimeter

https://brainly.com/question/19819849

#SPJ1

Since the range of observed values is 1, which is less than two standard deviations away from 10, the observed value is not significantly different from the expected value and thus the number of girls in 10 births is not significantly low.

Standard deviation is a measure of how spread out numbers are in a data set. It is calculated by taking the square root of the variance. Variance is the average of the squared differences from the mean. Standard deviation provides an indication of how much variation there is in the data set, and is often used in statistical analysis.

The range rule of thumb is a statistical method used to determine whether a given phenomenon is significantly different from an expected value. It states that if the range of observed values is greater than two standard deviations of the expected value, then the observed values are significantly different from the expected value.

In this particular case, the expected value is 10 girls in 10 births, and the observed value is 1 girl in 10 births. Since the range of observed values is 1, which is less than two standard deviations away from 10, the observed value is not significantly different from the expected value and thus the number of girls in 10 births is not significantly low.

The range rule of thumb is one way to determine whether observed values are significantly different from expected values, but there are other methods available as well.

For more questions related to variance

https://brainly.com/question/25639778

#SPJ1

The width of the rectangle is 5 meters.

To find the width of the rectangle, let's use the formula for the area of a rectangle, which is:

Area = length x width

We know that the area of the rectangle is 65 square meters. We also know that the length of the rectangle is 8 meters more than the width. Let's call the width "w". Then, the length can be expressed as:

length = w + 8

Substituting this expression for length into the formula for the area, we get:

65 = (w + 8) x w

Simplifying and solving for w, we get:

w² + 8w - 65 = 0

Using the quadratic formula, we get:

w = (-8 ± √(8² + 4(1)(65))) / (2(1))

w = (-8 ± √(324)) / 2

w = (-8 ± 18) / 2

We take the positive value for w since the width cannot be negative:

w = (-8 + 18) / 2

w = 5

Find out more about the width of the rectangle

at brainly.com/question/27555801

#SPJ4

Answer:

Step-by-step explanation:

In approximately 11.41% of years, the rainfall will be between 50 and 70 centimeters in that town.

To solve this problem, we need to find the percentage of years where the rainfall is between 50 and 70 centimeters. We can do this by standardizing the rainfall values and using a standard normal distribution table.

First, we need to standardize the rainfall values of 50 and 70 centimeters using the formula

z = (x - μ) / σ

where

z is the standardized value

x is the rainfall value

μ is the mean

σ is the standard deviation

For x = 50

z = (50 - 95) / 28

z = -1.607

For x = 70

z = (70 - 95) / 28

z = -0.893

Next, we use a standard normal distribution table or calculator to find the area under the curve between these two standardized values. This represents the percentage of years where the rainfall is between 50 and 70 centimeters.

Using a standard normal distribution table, we can find that the area under the curve between z = -1.607 and z = -0.893 is 0.1141. This means that approximately 11.41% of years will have rainfall between 50 and 70 centimeters in this town.

Learn more about standard deviation here

brainly.com/question/29262399

#SPJ4

Answer:

3

Step-by-step explanation:

Number of people in the choir = 80

Number of women = half of 80 = 40

Number of men in the choir is ¼ of the women = 40/4 = 10

Number of men plus women = 10 +40 = 50

Number of children = 80 - 50 = 30

Ratio of children to men = n:1 = 30:10

Divide both sides by 10

30:10 = 3:1

n = 3

A horizontal curve is to be designed with a 2000 feet radius. The curve has a tangent length of 400 feet and its pi is located at station 103+00. Determine the stationing of the PT.

A horizontal curve is a curve that is used to provide a transition between two tangent sections of a roadway. To connect two tangent road sections, horizontal curves are used. Horizontal curves are defined by a radius and a degree of curvature. The curve's radius is given as 2000 feet. The tangent length is 400 feet.

The pi is located at station 103+00.

To determine the stationing of the PT, we must first understand what the "pi" means. PC or point of curvature, PT or point of tangency, and PI or point of intersection are the three primary geometric features of a horizontal curve. The point of intersection (PI) is the point at which the back tangent and forward tangent of the curve meet. It is an important point since it signifies the location of the true beginning and end of the curve. To calculate the PT station, we must first determine the length of the curve's arc. The formula for determining the length of the arc is as follows:

L = 2πR (D/360)Where:

L = length of the arc in feet.

R = the radius of the curve in feet.

D = the degree of curvature in degrees.

PI (103+00) indicates that the beginning of the curve is located 103 chains (a chain is equal to 100 feet) away from the road's reference point. This indicates that the beginning of the curve is located 10300 feet from the road's reference point. Now we need to calculate the degree of curvature

:Degree of curvature = 5729.58 / R= 5729.58 / 2000= 2.8648 degrees. Therefore, the arc length is:

L = 2πR (D/360)= 2π2000 (2.8648/360)= 301.6 feet.

The length of the curve's chord is equal to the length of the tangent, which is 400 feet. As a result, the length of the curve's long chord is: Long chord length = 2R sin (D/2)= 2 * 2000 * sin(2.8648/2)= 152.2 feet To determine the stationing of the PT, we can use the following formula: PT stationing = PI stationing + Length of curve's long chord= 10300 + 152.2= 10452.2Therefore, the stationing of the PT is 10452+2.

A horizontal curve is to be designed with a 2000 feet radius : https://brainly.com/question/31078631

#SPJ11

Answer:

Step-by-step explanation:

To find out how much more fabric is required for the chair than the footstool, we need to subtract the amount of fabric required for the footstool from the amount of fabric required for the chair.

The amount of fabric required for the chair is 5/7 of a yard.

The amount of fabric required for the footstool is 2/3 of a yard.

So to find the difference, we need to subtract:

5/7 - 2/3

To do this, we need to find a common denominator, which is 21 in this case. We get:

(15/21) - (14/21) = 1/21

Therefore, Aron needs 1/21 more yard of fabric to cover the chair than the footstool.

The probability that a person chosen at random has run a red light in the last year can be calculated by taking the number of people who said “yes” to running a red light and dividing it by the total number of people in the group.

For example, if 10 people said “yes” and 20 said “no”, the probability of a person chosen at random running a red light in the last year is 10/30, or 1/3.

The probability of an event happening is calculated using the formula:

Probability = Number of Favorable Outcomes / Total Number of Outcomes

In this case, the favorable outcome is running a red light in the last year, and the total number of outcomes is the total number of people asked.

To calculate the probability, we take the number of people who said “yes” to running a red light in the last year and divide it by the total number of people in the group. In our example, 10/30 = 1/3, so the probability that a person chosen at random has run a red light in the last year is 1/3.

In conclusion, the probability of a person chosen at random having run a red light in the last year is calculated by taking the number of people who responded “yes” and dividing it by the total number of people in the group.

See more about probability at: https://brainly.com/question/14633532

#SPJ11

we will use the Pythagorean theorem, which states that in a right triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides.

In this case, the distance across the lake is the hypotenuse, and the given measurements a and b are the other two sides.

Solution:

1. Write the Pythagorean theorem:

c² = a² + b²,

where c is the distance across the lake.
2. Substitute the given measurements:

c² = (2.62)² + (3.51)²
3. Calculate the squares:

c² = 6.8644 + 12.3201
4. Add the squared values:

c² = 19.1845
5. Find the square root of the sum:

c = √19.1845
6. Calculate the distance:

c ≈ 4.38 miles

The distance across the lake is approximately 4.38 miles

To know more about Pythagorean theorem:

https://brainly.com/question/14930619

#SPJ11

Ben's net earnings after 5 years are $171,563.23, and Arthur's net earnings after 5 years are $163,534.49.

To calculate their net earnings, we first need to calculate their total earnings from their investments, and then subtract their initial investments.

For Ben:

Using the compound interest formula: A = P(1 + r/n)^(nt)

A = future value of the investment

P = initial principal (investment)

r = annual interest rate (as a decimal)

n = number of times interest is compounded per year

t = number of years

A = 500,000(1 + 0.06/12)^(12 * 5)

A ≈ $671,563.23

Net earnings for Ben: $671,563.23 - $500,000 = $171,563.23

For Arthur:

A = 600,000(1 + 0.05/4)^(4 * 5)

A ≈ $763,534.49

Net earnings for Arthur: $763,534.49 - $600,000 = $163,534.49

Ben's net earnings after 5 years are $171,563.23, and Arthur's net earnings after 5 years are $163,534.49.

Read more about compound interest here:

https://brainly.com/question/24274034

#SPJ1

Ben invested $500,000 at an annual interest rate of 6%, compounded monthly, for 5 years. Arthur invested $600,000 at an annual interest rate of 5%, compounded quarterly, for 5 years. What are their net earnings after 5 years?

Answer: 3.9b−2.6

Step-by-step explanation: Hope this helps

Answer:

1.3b

Step-by-step explanation:

The equation is -2.6+3.9b. A negative number acts like subtraction, so we would subtract 2.6 from 3.9 to get 1.3. The b is still there, and we don't know what it is, so we simplify the equation to 1.3b.

Sorry, this explanation isn't the best. Hope it helped! :)

There are 5²⁵ possible ways to select 25 cans of soda from 5 types, while there are [5¹⁸] (25 choose 7) possible ways to select 25 cans with at least 7 Dr. Peppers, and only [3²²] (25 choose 3) possible ways to select 25 cans with only 3 Dr. Peppers available.

(a) Since there are five types of soda and we are selecting 25 cans, we can choose any type of soda for each can. Therefore, the number of ways to select 25 cans of soda is 5²⁵.

(b) If we must include at least seven Dr. Peppers, then we can choose the remaining 18 cans from any of the five types of soda (including Dr. Pepper). We can choose 7 Dr. Peppers in (25 choose 7) ways. Therefore, the number of ways to select 25 cans of soda with at least seven Dr. Peppers is (25 choose 7) [5¹⁸].

(c) If there are only three Dr. Peppers available, then we must choose all three Dr. Peppers and select the remaining 22 cans from the four types of soda (excluding Dr. Pepper). We can choose the remaining 22 cans in 4²² ways. Therefore, the number of ways to select 25 cans of soda with only three Dr. Peppers available is 3 [4²²].

Learn more about Combinatorics here: brainly.com/question/13261685

#SPJ4

Complete question:

From an unlimited selection of five types of soda, one of which is Dr. Pepper, you are putting 25 cans on a table.

(a) Determine the number of ways you can select 25 cans of soda.

(b) Determine the number of ways you can select 25 cans of soda if you must include at least seven Dr. Peppers.

(c) Determine the number of ways you can select 25 cans of soda if it turns out there are only three Dr. Peppers available.

Therefore, the inequality that can be used to determine p, the maximum number of people who can go to the amusement park, is p ≤ 30.

In mathematics, inequalities are statements that compare two values or expressions and indicate whether they are equal, greater than, or less than each other. An inequality is typically represented by a symbol, such as "<" (less than), ">" (greater than), "<=" (less than or equal to), ">=" (greater than or equal to), or "≠" (not equal to).

Given by the question.

Let's assume that the maximum number of people that can go to the amusement park is p. The cost of parking is $8.75, and the cost of admission for each person is $15.50.

Then, the total cost for p people can be calculated as:

Total cost = (Cost of parking) + (Cost of admission per person x number of people)

Total cost = $8.75 + $15.50p

The group has no more than $480 to spend, so we can set up an inequality:

Total cost ≤ $480

$8.75 + $15.50p ≤ $480

Subtracting $8.75 from both sides:

$15.50p ≤ $471.25

Dividing both sides by $15.50:

p ≤ 30.35

Since the number of people cannot be a decimal, we round down to the nearest whole number: p ≤ 30.

To learn more about decimal:

https://brainly.com/question/30958821

#SPJ1

It takes 3.1 hour  for half of the drug dose to be left in the body.

In the metric system the unit measurement of mass is known as mg .

mg is equal to one thousandth of a gram ie.1/1000. The unit is often used in medical field for weighing out small quantities of  ingredients.

prons

it is precise and it can be used to measure small quantities of items.

It is easy to convert mg to other units of measure.

cons:

It is a very small unit of measurement, it is difficult to measure the values accurately.

It is also a very commonly used unit of measurement, it get easily  confuse with other units

10*1/2=10(0.8)^t

0.8^t=1/2

t=log0.8*1/2

t=3.1

to know more about milligram visit

https://brainly.com/question/30404126

#SPJ1

Answer: 7x - 7y + 21

Step-by-step explanation:

7( x - y + 3) = 7x - 7y + 21

Answer:

33

Step-by-step explanation:

43-10=33 sarah has 33 bananas ledt

Step-by-step explanation:

The sum of 2 and 2 can be derived using basic arithmetic operations.

Starting with 2, we can add 1 to get 3:

2 + 1 = 3

Then, we can add another 1 to get 4:

3 + 1 = 4

Therefore, the derivation of 2 + 2 is:

2 + 2 = (2 + 1) + 1 = 3 + 1 = 4

Hence, 2 + 2 is equal to 4.

Answer:

4

Step-by-step explanation:

The equation of the line in slope-intercept form is y = 6x + 55.

Equations can involve variables, which are placeholders for unknown values that we wish to find. For example, the equation x + 3 = 7 asserts that the value of x plus 3 is equal to 7. We can solve for x by subtracting 3 from both sides of the equation, obtaining x = 4.

Equations can be linear or nonlinear, and they can involve one or more variables. They can be represented in various forms, such as standard form, slope-intercept form, or quadratic form.

To find the equation of the line in point-slope form, we need to first find the slope of the line. We can use any two points from the table to find the slope using the formula:

slope = (change in y)/(change in x)

Let's use the first and last points in the table:

slope = (295 - 175)/(40 - 20) = 120/20 = 6

Now we can use the point-slope form of the equation of a line:

y - y1 = m(x - x1)

where m is the slope and (x1, y1) is any point on the line. Let's use the first point (20, 175):

y - 175 = 6(x - 20)

To write this equation in slope-intercept form, we need to isolate y:

y - 175 = 6x - 120

y = 6x + 55

So the equation of the line in slope-intercept form is y = 6x + 55.

To know more about line visit:

https://brainly.com/question/28947895

#SPJ1

As per the combination concept, there are 735,471 ways to choose 16 shows from a set of 24.

To find the number of ways to choose 16 shows from a set of 24, we can use the formula for combinations, which is:

ⁿCₓ = n! / x!(n-x)!

Where n is the total number of objects in the set (in this case, 24), and x is the number of objects we want to choose (in this case, 16). The exclamation mark (!) denotes the factorial function, which means multiplying the number by all positive integers less than itself.

Plugging in the numbers, we get:

²⁴C₁₆ = 24! / 16!(24-16)! = 735471

To know more about combination here

https://brainly.com/question/28998705

#SPJ4

we have found that in the given right triangle with sides 10, 24, and 26, the tangent of the larger acute angle (angle B) is 2.4.

In a right triangle, the tangent of an acute angle is defined as the ratio of the length of the opposite side to the length of the adjacent side. Let us label the sides of the right triangle as follows:

The hypotenuse (the longest side) is 26

One of the acute angles (let's call it angle A) has opposite side length of 10

The other acute angle (let's call it angle B) has opposite side length of 24

To find the tangent of the larger acute angle, which is angle B, we use the formula:

tan(B) = opposite / adjacent

In this case, the opposite side of angle B is 24, and the adjacent side is 10. So we have:

tan(B) = 24 / 10 = 2.4

Therefore, the tangent of the larger acute angle (angle B) is 2.4.

This means that if we draw a line that is tangent to the circle with radius 10 centered at the vertex of angle B, the length of that line will be 24. This is a geometric interpretation of the tangent function, where the tangent of an angle is the length of a line tangent to the unit circle at that angle.

In conclusion, we have found that in the given right triangle with sides 10, 24, and 26, the tangent of the larger acute angle (angle B) is 2.4.

To know more about tangent  click here:

brainly.com/question/19064965

#SPJ4

Slope of each graph are [tex]\frac{6}{5}[/tex],[tex]\frac{-1}{3}[/tex] and 1 respectively.

Slope of a line in mathematics is defined as the ratio of the change in the y coordinate w.r.t the change in the x coordinate.

Both the change in the y-coordinate and the net change in the x-coordinate are denoted by y₂-y₁ and x₂-x₁, respectively.

Thus, the formula for the change in y-coordinate with regard to the change in x-coordinate is

m=y₂-y₁/ x₂-x₁

Taking two points as per observation

Point1: (x₁ y₁)=(0,-3)

Point2:(x₂, y₂)=(5/2,0)

Slope of line=y₂-y₁/ x₂-x₁

=[tex]\frac{0+3}{5/2-0}[/tex]

=[tex]\frac{6}{5}[/tex]

Taking two points as per observation

Point1: (x₁ y₁)=(0,3)

Point2:(x₂, y₂)=(2,2)

Slope of line=y2-y1/x2-x1

=[tex]\frac{2-3}{2-0}[/tex]

=-⅓

Taking two points as per observation

Point1: (x₁ y₁)=(-2,0)

Point2:(x₂, y₂)=(0,2)

Slope of line=y2-y1/x2-x1

=[tex]\frac{2-0}{0+2}[/tex]

=1

Hence, Slope of each graph are 6/5,-⅓ and 1 respectively.

to know more about lines, visit:

https://brainly.com/question/30003330

#SPJ1

Carter has 13 dimes in his piggy bank

To solve this equation, we need to use the distributive property to simplify the equation:
(x dimes x 10 cents) + (37-x nickels x 5 cents) = $3.10
We can then solve for the number of dimes by isolating the dimes on one side of the equation:
x dimes x 10 cents = $3.10 - (37-x nickels x 5 cents),By dividing both sides of the equation by 10 cents, we can solve for the number of dimes, x:
x dimes = ($3.10 - (37-x nickels x 5 cents)) / 10 cents

Plugging in the value of 37 coins and solving the equation, we get:
x dimes = (3.10 - (37 -x nickels x 5 cents)) / 10 cents
x dimes = (3.10 - 185 + 5x) / 10 centsx dimes = (3.10 - 180) / 10 centsx dimes = 1.30 / 10 centsx dimes = 13 dimes
Therefore, Carter has 13 dimes in his piggy bank.

To know more about linear equation click here:

https://brainly.com/question/13738061

#SPJ11

Answer: 3

Step-by-step explanation: I just know

Similarly, there are 10 choices for the first number, 9 choices for the second number, and 8 choices for the third number. Therefore, the total number of possibilities is[tex]26 × 25 × 24 × 23 × 22 × 10 × 9 × 8 = 14,776,320[/tex] possibilities.

Fundamental Counting Principle and how to count with and without replacement.The Fundamental Counting Principle (FCP) states that if there are m ways to perform an event and n ways to perform a second event, then there are m × n ways to perform both events. For example, suppose there are 2 shirts, 3 pants, and 4 pairs of shoes in your closet. Using the FCP, you can calculate the number of outfit combinations: 2 × 3 × 4 = 24.If you are allowed to use characters more than once (with replacement), the number of different possibilities for a password can be calculated by multiplying the number of choices for each character type. There are 26 lowercase letters, so there are 26 choices for the first letter, 26 choices for the second letter, and so on. Similarly, there are 10 digits, so there are 10 choices for each number.

Therefore, the total number of possibilities is [tex]26 × 26 × 26 × 26 × 26 × 10 × 10 × 10 = 26^5 × 10^3 = 11,881,376,000[/tex] possibilities.If you may only use each letter or number one time, then you cannot repeat any choices. Therefore, the number of possibilities is reduced. There are 26 choices for the first letter, 25 choices for the second letter (since one has already been used), and so on.

for such more questions on no of combinations

https://brainly.com/question/29089154

#SPJ11

250 is the total surface area of the solid.

How do you determine surface area?

The whole surface of a three-dimensional form is referred to as its surface area. The surface area of a cuboid with six rectangular faces may be calculated by adding the areas of each face.

                         Instead, you may write out the cuboid's length, width, and height and apply the formula surface area (SA)=2lw+2lh+2hw.

Each side of a cube with side length = 5  has an area of 25; the overall area is 6 x 25 = 150

A cube with sides of length 5 has an area of 25 on each side, making its overall area 6 x 25 or 150.

Both have a combined area of 150 + 150 = 300

300 - 25 - 25 = 250 is the result from each of the two cubes.

Learn more about Surface area

brainly.com/question/29298005

#SPJ1

the number of more 4's printed than 8's is 188 - 59 = 129.

We can approach this problem by counting the number of times the digit 4 appears and the number of times the digit 8 appears in the page numbers from 1 to 488.

First, let's count the number of times the digit 4 appears. We can break down the counting into three cases:

The digit 4 appears in the units place (page numbers 4, 14, 24, ..., 484): there are 49 such page numbers (from 4 to 484, incrementing by 10).

The digit 4 appears in the tens place (page numbers 40 to 49, 140 to 149, ..., 440 to 449): there are 50 such page numbers.

The digit 4 appears in the hundreds place (page numbers 400 to 488): there are 89 such page numbers.

Thus, the total number of times the digit 4 appears is 49 + 50 + 89 = 188.

Next, let's count the number of times the digit 8 appears. We can break down the counting into two cases:

The digit 8 appears in the tens place (page numbers 80 to 89, 180 to 189, ..., 480 to 489): there are 50 such page numbers.

The digit 8 appears in the hundreds place (page numbers 800 to 880): there are 9 such page numbers.

Thus, the total number of times the digit 8 appears is 50 + 9 = 59.

Therefore, the number of more 4's printed than 8's is 188 - 59 = 129.

learn more about number here

https://brainly.com/question/10547079

#SPJ4

The probability that the coin will land on the same side in all three tosses is 1/8.

There are two possible outcomes for each coin flip: heads or tails. Therefore, there are 2 × 2 × 2 = 8 possible outcomes for flipping a coin three times in a row.To find the probability that the coin will land on the same side in all three tosses, we need to count the number of outcomes that satisfy this condition.

There are only two such outcomes: either all three tosses are heads or all three tosses are tails. Therefore, the probability of this happening is 2/8 or 1/4.But we are asked for the probability that the coin will land on the same side in all three tosses, not just one specific side.

Therefore, we need to divide our previous result by 2 (the number of sides of the coin) to get the final answer: 1/4 ÷ 2 = 1/8. The probability that the coin will land on the same side in all three tosses is 1/8.

To know more about probability click on below link:

https://brainly.com/question/30034780#

#SPJ11